Direction of the power flow of harmonics
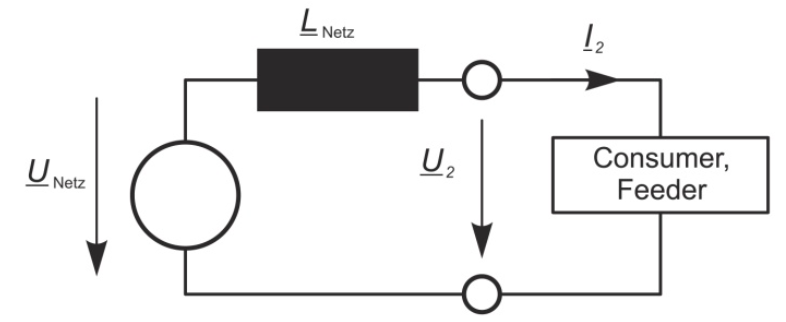
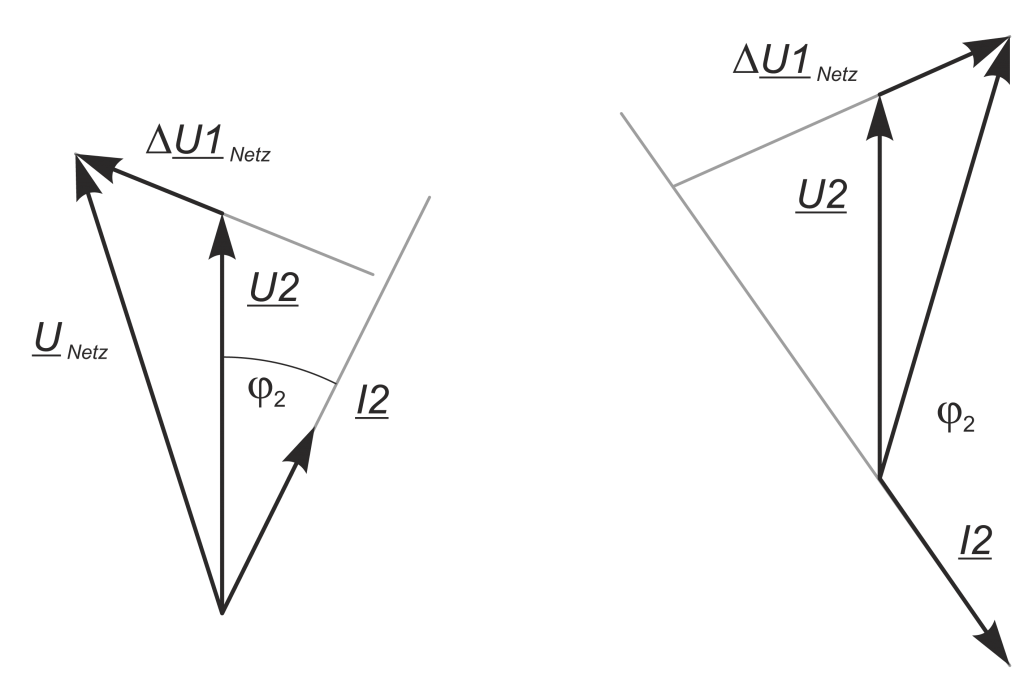
The direction of the power flow of harmonics is determined by the sign of the active power. The figure shows the equivalent circuit of a network/consumer configuration (single phase); the figures shown the corresponding vector diagrams for the two energy flow directions, energy consumption and energy recovery.
The active power is calculated with pure sinusoidal waveforms:
P_{2} = U_{2} * I_{2} * cosφ_{2}In the angular range 0 ≤ φ2 ≤ 90° and 270° ≤ φ2 ≤ 0° there is a consumer structure and P receives a positive sign.
For φ2 = 90° ≤ φ2 ≤ 270°, P is calculated with a negative sign, so power can be supplied.
Harmonic generator in a clean network
The consumer is connected in a “clean” sine wave network. At the measurement point, the Fourier transform provides both the amplitude and the angle of the respective harmonics. If the angle between the current and the voltage is > ± 90°, with these harmonics the consumer acts as a generator, i.e. it injects harmonics into the network (contaminates the network).
Sinusoidal network voltage – current affected by harmonics
From the definition of the active power, with a current affected by harmonics the corresponding active power is given by:
P = U * \frac{i_{1}}{\sqrt{2}}* cosφ_{1}where
i_{(t)}*sin(ω_{1}t) + \sum^{∞}_{h=2}sin(h * ω_{1}t + φ_{h})It is apparent from this that only the fundamental frequency of the current i1(t) determines the active power.
Current and voltage are affected by harmonics
With the approach to the non-sinusoidal current load (i.e. Current I is composed of the fundamental frequency and harmonics), calculating the active power is more complex.
In this case, analogous to the current, the voltage also has a fundamental frequency and harmonics.
u_{(t)} = u_{(1)}*sin(ω_{1}t+φ_{u1}) + \sum^{∞}_{h=2} u_{h} * sin(h * ω_{1}t + φ_{uh}) i_{(t)} = i_{(1)}*sin(ω_{1}t+φ_{i1}) + \sum^{∞}_{h=2}i_{h} * sin(h * ω_{1}t + φ_{ih}) Only when the voltage harmonics and the current harmonics are at the same frequency do they combine to produce an active power.