Tension homopolaire dans les réseaux triphasés
En cas de fonctionnement équilibré du réseau et d’inégalité des impédances dans le circuit consommateur, les tensions de phase des deux circuits, et donc les points neutres, ne sont plus congruents.
Entre les points neutres, il existe une différence de tension, appelée tension homopolaire, dont l’importance dépend de l’inégalité des impédances dans le circuit consommateur.
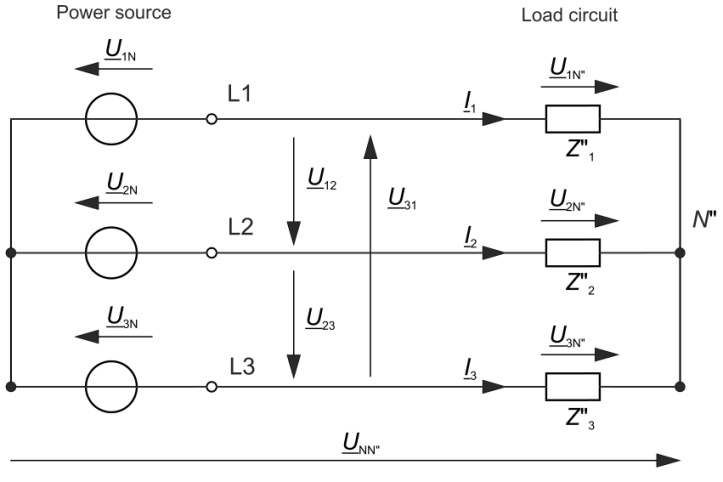
Réseau triphasé à trois fils
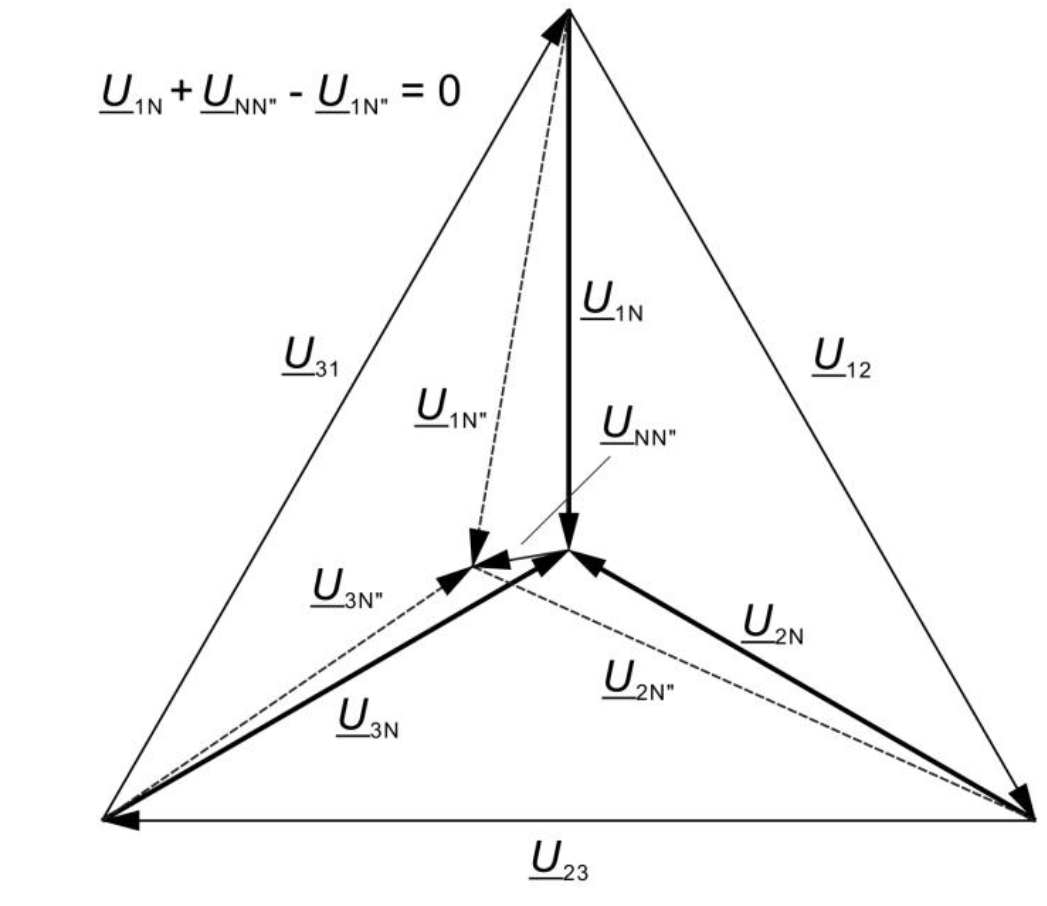
La somme géométrique des valeurs effectives complexes des courants de phase (voir figure 2) est nulle et donc :
\frac{\underline{U}_{1N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{1}}}+\frac{\underline{U}_{2N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{2}}}+\frac{\underline{U}_{3N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{3}}}=0En conséquence :
\underline{U}_{NN''} = \frac{1}{3}[(\underline{U}_{1N''}+\underline{U}_{2N''}+\underline{U}_{3N''})-(\underline{U}_{1N}+\underline{U}_{2N}+\underline{U}_{3N})]En cas de fonctionnement symétrique du réseau, U1N + U2N + U3N = 0 et donc la tension UNN » est égale à la composante zéro U0, qui est donc également appelée tension homopolaire.
\underline{U}_{NN''}=\frac{1}{3}(\underline{U}_{1N''}+\underline{U}_{2N''}+\underline{U}_{3N''})Et puis aussi :
\underline{U}_{NN''}=-\frac{1}{3}[\underline{I}_{1}(\underline{Z}^{''}_{2}-\underline{Z}^{''}_{1})+\underline{I}_{3}(\underline{Z}^{''}_{2}-\underline{Z}^{''}_{3})]L’influence
L’effet sur la tension homopolaire d’impédances inégales dans le circuit du consommateur (qui provoquent à leur tour des courants asymétriques) est directement reconnaissable à partir de cette équation.