Zero sequence voltage in three-phase networks
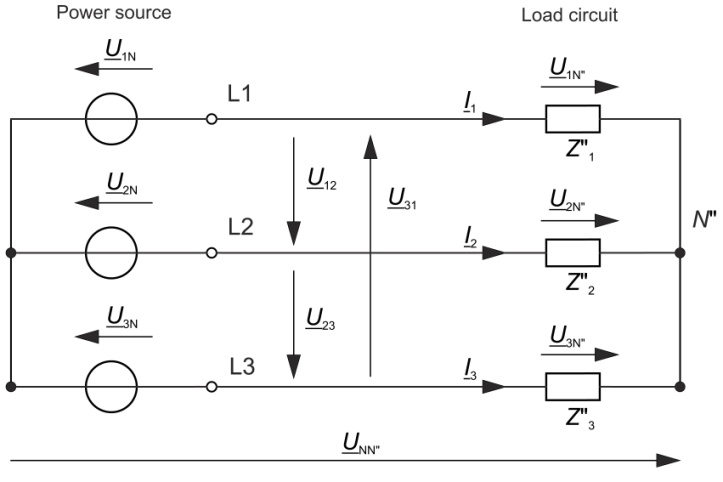
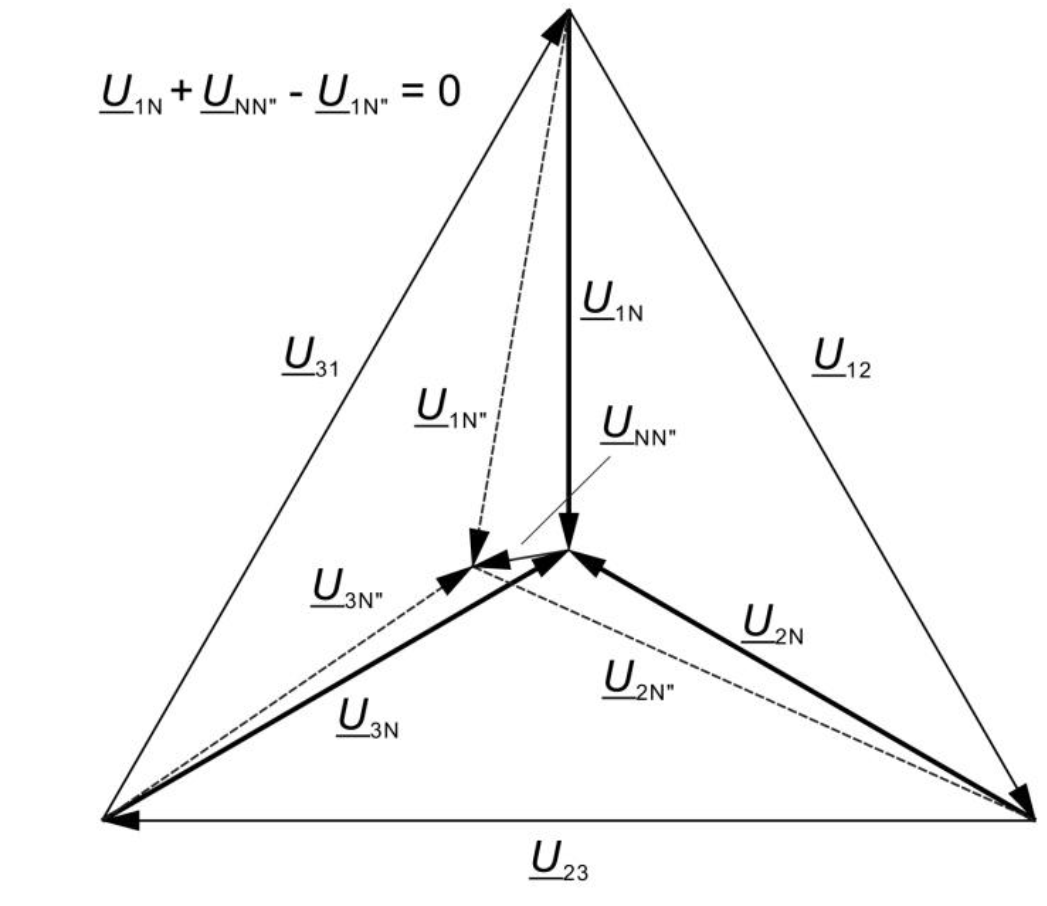
With balanced network operation and inequality of the impedances in the consumer circuit, the phase voltages of the two circuits, and thus the neutral points are no longer congruent.
Between the neutral points, there is a voltage difference, which is referred to as the zero sequence voltage and the amount depends on the inequality of the impedances in the consumer circuit.
Three-phase three-wire network
The geometric sum of the complex effective values of the phase currents (see Figure 2) is zero and thus:
\frac{\underline{U}_{1N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{1}}}+\frac{\underline{U}_{2N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{2}}}+\frac{\underline{U}_{3N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{3}}}=0As a result:
\underline{U}_{NN''} = \frac{1}{3}[(\underline{U}_{1N''}+\underline{U}_{2N''}+\underline{U}_{3N''})-(\underline{U}_{1N}+\underline{U}_{2N}+\underline{U}_{3N})]With symmetrical network operation U1N + U2N + U3N = 0 and thus the voltage UNN“ equal to the zero component U0, which is therefore also called the zero sequence voltage.
\underline{U}_{NN''}=\frac{1}{3}(\underline{U}_{1N''}+\underline{U}_{2N''}+\underline{U}_{3N''})Then also:
\underline{U}_{NN''}=-\frac{1}{3}[\underline{I}_{1}(\underline{Z}^{''}_{2}-\underline{Z}^{''}_{1})+\underline{I}_{3}(\underline{Z}^{''}_{2}-\underline{Z}^{''}_{3})]The influence
The effect on the zero sequence voltage of unequal impedances in the consumer circuit (which in turn cause asymmetric currents) is directly recognizable from this equation.