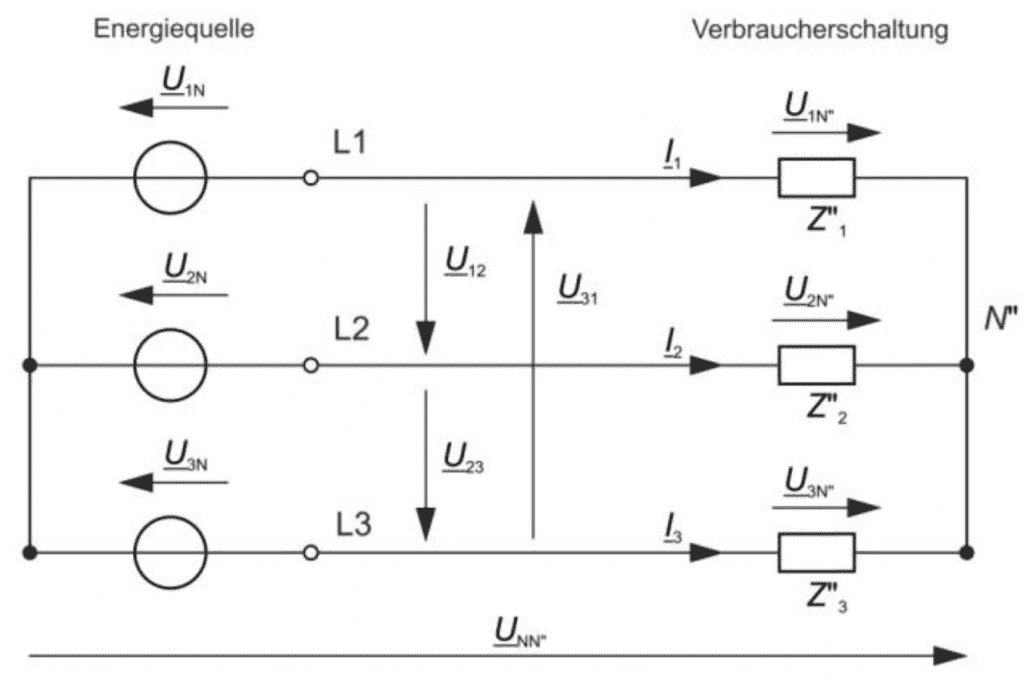
Verlagerungsspannung im Drehstromnetz
Bei symmetrischem Netzbetrieb und Ungleichheit der Impedanzen in der Verbraucherschaltung sind die Sternspannungen der beiden Schaltungen und somit auch die Sternpunkte nicht mehr deckungsgleich.
Zwischen den Sternpunkten besteht eine Spannungsdifferenz, die als Verlagerungsspannung bezeichnet wird und deren Höhe von der Ungleichheit der Impedanzen in der Verbraucherschaltung abhängt.
Drehstrom-Dreileiternetz
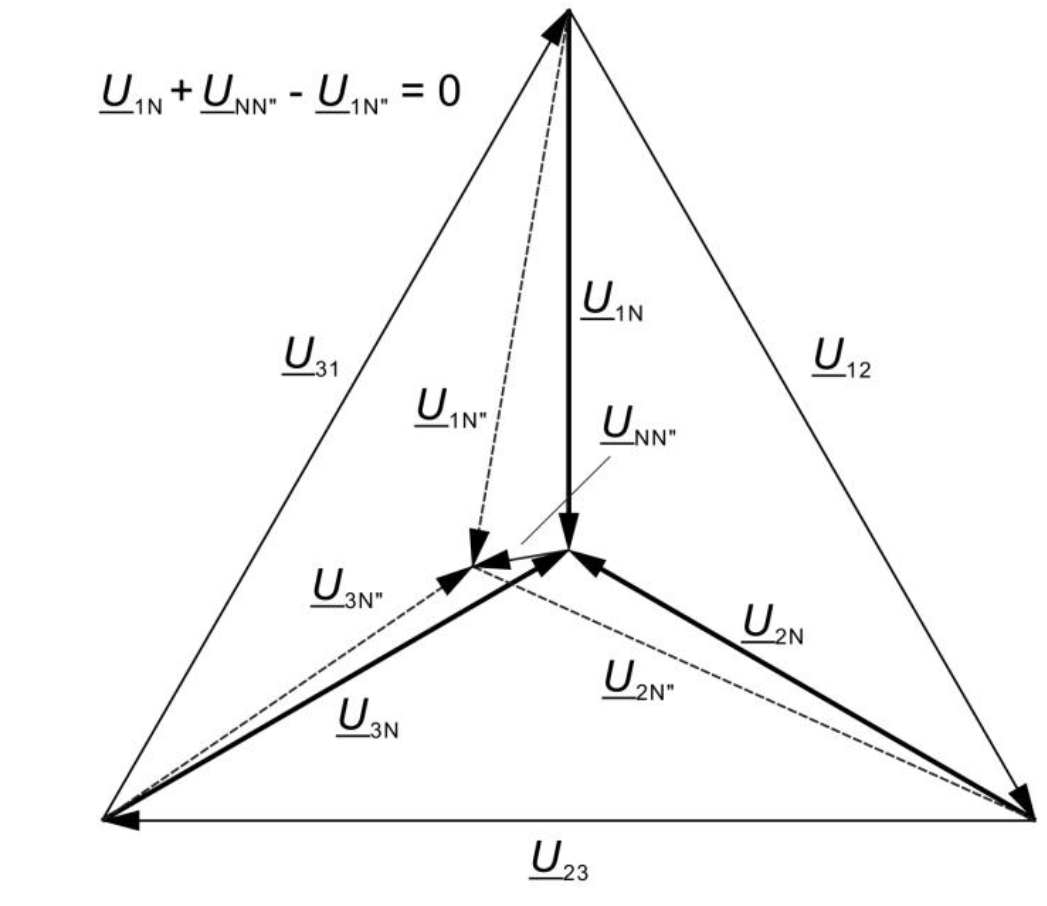
Die geometrische Summe der komplexen Effektivwerte der Leiterströme (siehe Bild 2) ist null und somit gilt:
\frac{\underline{U}_{1N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{1}}}+\frac{\underline{U}_{2N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{2}}}+\frac{\underline{U}_{3N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{3}}}=0Daraus ergibt sich:
\underline{U}_{NN''} = \frac{1}{3}[(\underline{U}_{1N''}+\underline{U}_{2N''}+\underline{U}_{3N''})-(\underline{U}_{1N}+\underline{U}_{2N}+\underline{U}_{3N})]Bei symmetrischem Netzbetrieb ist U1N+ U2N+ U3N = 0 und somit die Spannung UNN“ gleich der Nullkomponente U0, die deshalb ebenso als Verlagerungsspannung bezeichnet wird.
\underline{U}_{NN''}=\frac{1}{3}(\underline{U}_{1N''}+\underline{U}_{2N''}+\underline{U}_{3N''})Dann gilt auch:
\underline{U}_{NN''}=-\frac{1}{3}[\underline{I}_{1}(\underline{Z}^{''}_{2}-\underline{Z}^{''}_{1})+\underline{I}_{3}(\underline{Z}^{''}_{2}-\underline{Z}^{''}_{3})]Der Einflusseffekt
Der Einflusseffekt auf die Verlagerungsspannung von ungleichen Impedanzen der Verbraucherschaltung (die wiederum ungleiche Stromstärken bewirken) ist bei dieser Formel direkt erkennbar.