Tensión homopolar en redes trifásicas
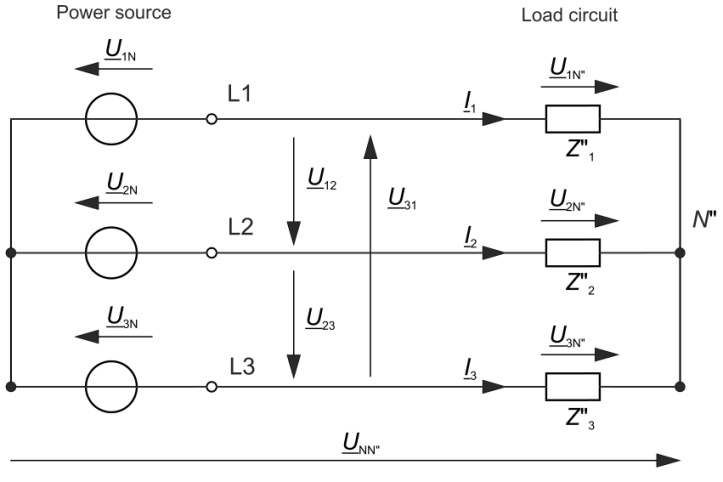
Con el funcionamiento equilibrado de la red y la desigualdad de las impedancias en el circuito de consumo, las tensiones de fase de los dos circuitos y, por tanto, los puntos neutros dejan de ser congruentes.
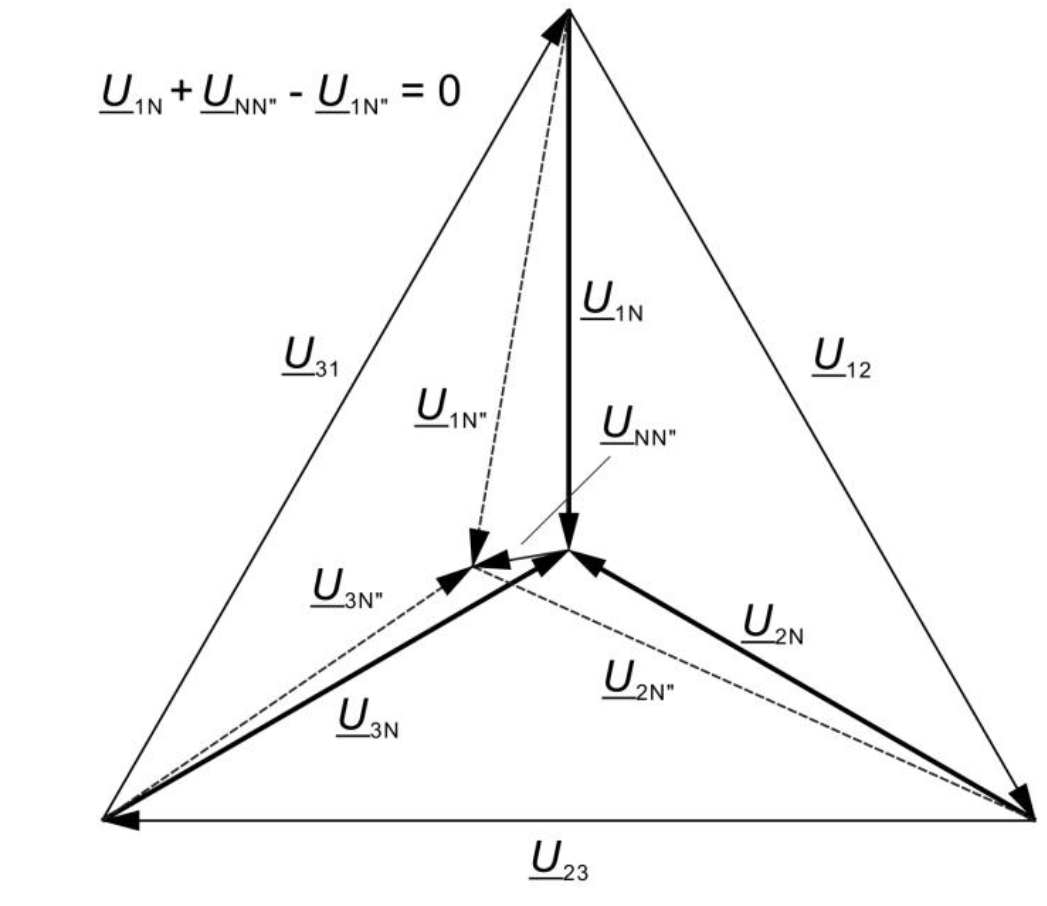
Entre los puntos neutros existe una diferencia de tensión, denominada tensión homopolar, cuya magnitud depende de la desigualdad de las impedancias en el circuito de consumo.
Red trifásica de tres hilos
La suma geométrica de los valores efectivos complejos de las corrientes de fase (véase la figura 2) es cero y, por tanto:
\frac{\underline{U}_{1N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{1}}}+\frac{\underline{U}_{2N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{2}}}+\frac{\underline{U}_{3N}+{\underline{U}_{NN''}}}{{\underline{Z}''_{3}}}=0Como resultado:
\underline{U}_{NN''} = \frac{1}{3}[(\underline{U}_{1N''}+\underline{U}_{2N''}+\underline{U}_{3N''})-(\underline{U}_{1N}+\underline{U}_{2N}+\underline{U}_{3N})]Con funcionamiento simétrico de la red U1N + U2N + U3N = 0 y, por tanto, la tensión UNN» igual a la componente cero U0, que también se denomina, por tanto, tensión homopolar.
\underline{U}_{NN''}=\frac{1}{3}(\underline{U}_{1N''}+\underline{U}_{2N''}+\underline{U}_{3N''})Entonces también:
\underline{U}_{NN''}=-\frac{1}{3}[\underline{I}_{1}(\underline{Z}^{''}_{2}-\underline{Z}^{''}_{1})+\underline{I}_{3}(\underline{Z}^{''}_{2}-\underline{Z}^{''}_{3})]La influencia
El efecto sobre la tensión homopolar de impedancias desiguales en el circuito de consumo (que a su vez provocan corrientes asimétricas) es directamente reconocible a partir de esta ecuación.