Dirección del flujo de potencia de los armónicos
La dirección del flujo de potencia de los armónicos viene determinada por el signo de la potencia activa. La figura muestra el circuito equivalente de una configuración red/consumidor (monofásica); las figuras muestran los diagramas vectoriales correspondientes para las dos direcciones del flujo de energía, consumo de energía y recuperación de energía.
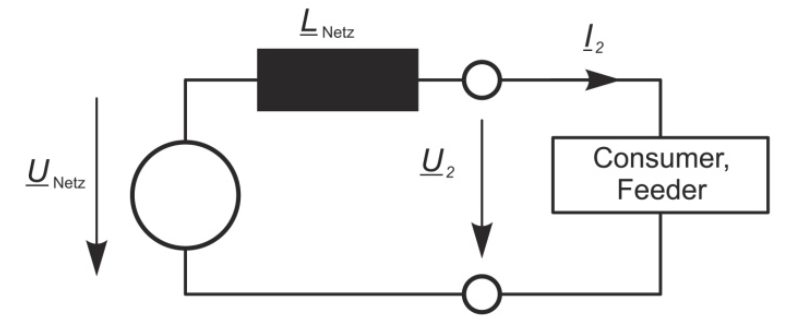
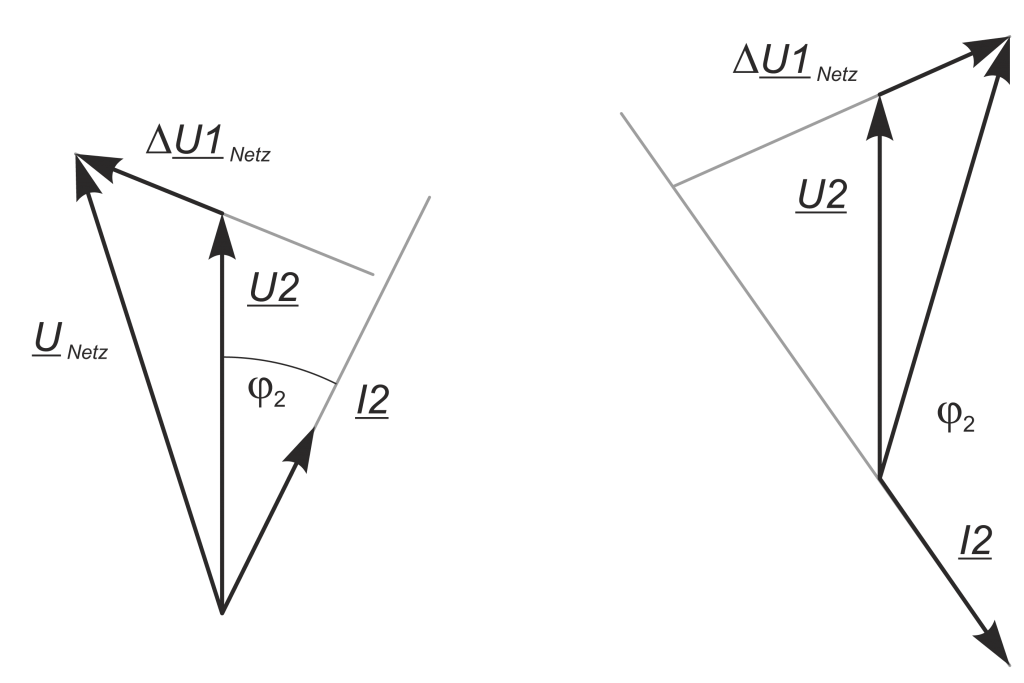
La potencia activa se calcula con formas de onda sinusoidales puras:
P_{2} = U_{2} * I_{2} * cosφ_{2}En el intervalo angular 0 ≤ φ2 ≤ 90° y 270° ≤ φ2 ≤ 0° hay una estructura de consumo y P recibe un signo positivo.
Para φ2 = 90° ≤ φ2 ≤ 270°, P se calcula con signo negativo, por lo que se puede suministrar energía.
Generador de armónicos en una red limpia
El consumidor está conectado a una red sinusoidal «limpia». En el punto de medición, la transformada de Fourier proporciona tanto la amplitud como el ángulo de los armónicos respectivos. Si el ángulo entre la corriente y la tensión es > ± 90°, con estos armónicos el consumidor actúa como generador, es decir, inyecta armónicos en la red limpia.
Tensión de red sinusoidal – corriente afectada por armónicos
A partir de la definición de la potencia activa, con una corriente afectada por armónicos la potencia activa correspondiente viene dada por:
P = U * \frac{i_{1}}{\sqrt{2}}* cosφ_{1}donde
i_{(t)}*sin(ω_{1}t) + \sum^{∞}_{h=2}sin(h * ω_{1}t + φ_{h})De ello se deduce que sólo la frecuencia fundamental de la corriente i1(t) determina la potencia activa.
La corriente y la tensión se ven afectadas por los armónicos
Con la aproximación a la carga de corriente no sinusoidal (es decir, la corriente I está compuesta por la frecuencia fundamental y los armónicos), el cálculo de la potencia activa es más complejo.
En este caso, análogamente a la corriente, la tensión también tiene frecuencia fundamental y armónicos.
u_{(t)} = u_{(1)}*sin(ω_{1}t+φ_{u1}) + \sum^{∞}_{h=2} u_{h} * sin(h * ω_{1}t + φ_{uh}) i_{(t)} = i_{(1)}*sin(ω_{1}t+φ_{i1}) + \sum^{∞}_{h=2}i_{h} * sin(h * ω_{1}t + φ_{ih}) Sólo cuando los armónicos de tensión y los armónicos de corriente están a la misma frecuencia se combinan para producir una potencia activa