Leistungsflussrichtung von Oberschwingungen
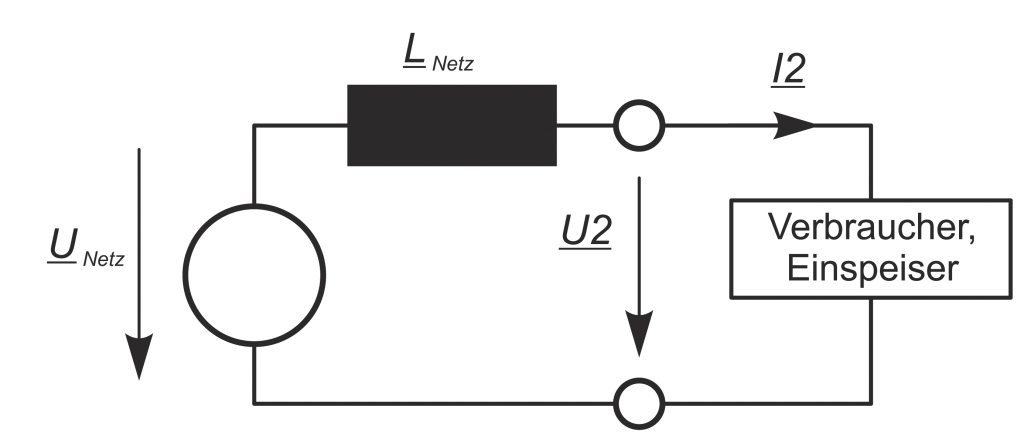
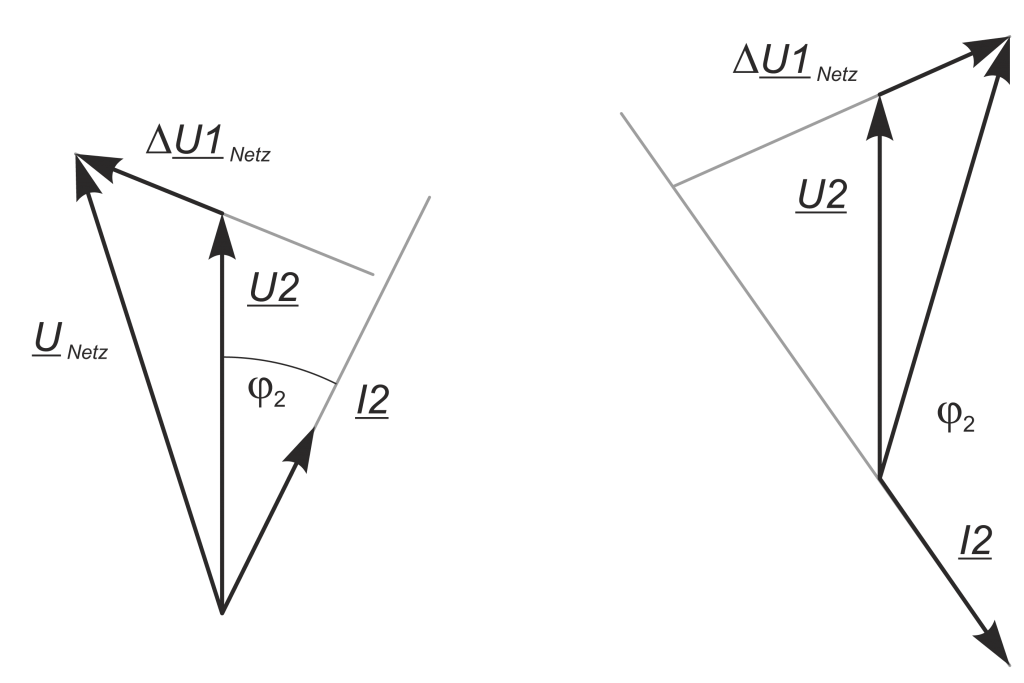
Die Leistungsflussrichtung von Oberschwingungen ist durch das Vorzeichen in der Wirkleistung bestimmt. Die Abbildung zeigt das Ersatzschaltbild einer Netz-/Verbraucheranordnung (einphasig); die Abbildungen zeigen die dazu gehörigen Zeigerdiagramme für zwei Energieflussrichtungen, Bezug und Rückspeisung.
Die Wirkleistung berechnet sich bei reinen sinus-förmigen Größen nach:
P_{2} = U_{2} * I_{2} * cosφ_{2}Im Winkelbereich 0 ≤ φ2 ≤ 90° sowie 270° ≤ φ2 ≤ 0° liegt eine Verbraucherstruktur vor und P erhält ein positives Vorzeichen. Für φ2 = 90° ≤ φ2 ≤ 270° errechnet sich P mit negativen Vorzeichen, es wird Leistung eingespeist.
Oberschwingungserzeuger in einem sauberen Netz
Der Verbraucher ist in einem “reinen“ Sinusnetz angeschlossen. Die Fouriertransformation liefert an den Messpunkten sowohl die Amplitude als auch den Winkel der jeweiligen Harmonischen. Ist der Winkel zwischen Strom und Spannung > ± 90° wirkt der Verbraucher bei dieser Harmonischen als Generator, d.h. er speist die Harmonische ins Netz (verseucht das Netz).
Sinusförmige Netzspannung – oberschwingungsbehafteter Strom
Aus der Definition der Wirkleistung ergibt sich mit einem oberschwingungsbehafteten Strom die Wirkleistung entsprechend:
P = U * \frac{i_{1}}{\sqrt{2}}* cosφ_{1}mit
i_{(t)}*sin(ω_{1}t) + \sum^{∞}_{h=2}sin(h * ω_{1}t + φ_{h})Daraus ist ersichtlich, dass nur die Stromgrundschwingung i1(t) die Wirkleistung bestimmt.
Strom und Spannung sind oberschwingungsbehaftet
Mit dem Ansatz der nicht sinusförmigen Strom-belastung (d.h. der Strom I besteht aus Grundschwingung und Oberschwingungen) wird die Leistungsberechnung aufwendiger.
Die Spannung ist in diesem Fall analog dem Strom mit Grundschwingung und Oberschwingungen zu beschreiben.
u_{(t)} = u_{(1)}*sin(ω_{1}t+φ_{u1}) + \sum^{∞}_{h=2} u_{h} * sin(h * ω_{1}t + φ_{uh}) i_{(t)} = i_{(1)}*sin(ω_{1}t+φ_{i1}) + \sum^{∞}_{h=2}i_{h} * sin(h * ω_{1}t + φ_{ih}) Nur Spannungsharmonische und Stromharmonische gleicher Frequenz ergeben zusammen eine Wirkleistung.