Allgemeine Infos
Bei der Parallelschaltung von Stromquellen gilt das Überlagerungsprinzip, wenn alle Betriebsmittel ein lineares Verhalten aufweisen. Dieses Verhalten ist bei Stromwandlern innerhalb des zulässigen Bürdenbereiches und unterhalb von einigen tausend Hertz gegeben. Dabei ist zu beachten, dass prinzipiell und gerätetechnisch nur zeitgleiche Momentanwerte addiert werden, nicht jedoch Effektivwerte! Durch den gemeinsamen Lastwiderstand RL von parallel geschalteten Stromwandlern fließt ein Strom der jeweils der arithmetischen Summe der Momentanwerte aller Ströme entspricht. Dabei wird vorausgesetzt, dass die Stromwandler eingeprägte Ströme liefern und die Frequenzgrenzen (höchste Ordnungszahl der Oberschwingungen) nicht überschritten werden. Die arithmetische Summe der Momentanwerte ist nicht nur abhängig vom Betrag, sondern auch vom Vorzeichen der einzelnen Ströme, so dass bei der Summierung die Polung der Stromquellen beachtet werden muss. Bei Wechselströmen mit gleicher Energieflussrichtung bezieht sich die Polung auf die Sekundäranschlüsse S1(k) und S2 (l) der Stromwandler.
Kurvenform des Summenstromes
Bei der Summierung von gleichfrequenten sinusförmigen Strömen hat die Kurvenform von iΣ wiederum einen sinus-förmigen Verlauf; bei Strömen mit ungleicher Frequenz ist die Kurvenform des Summenstromes iΣ nicht mehr sinus-förmig.
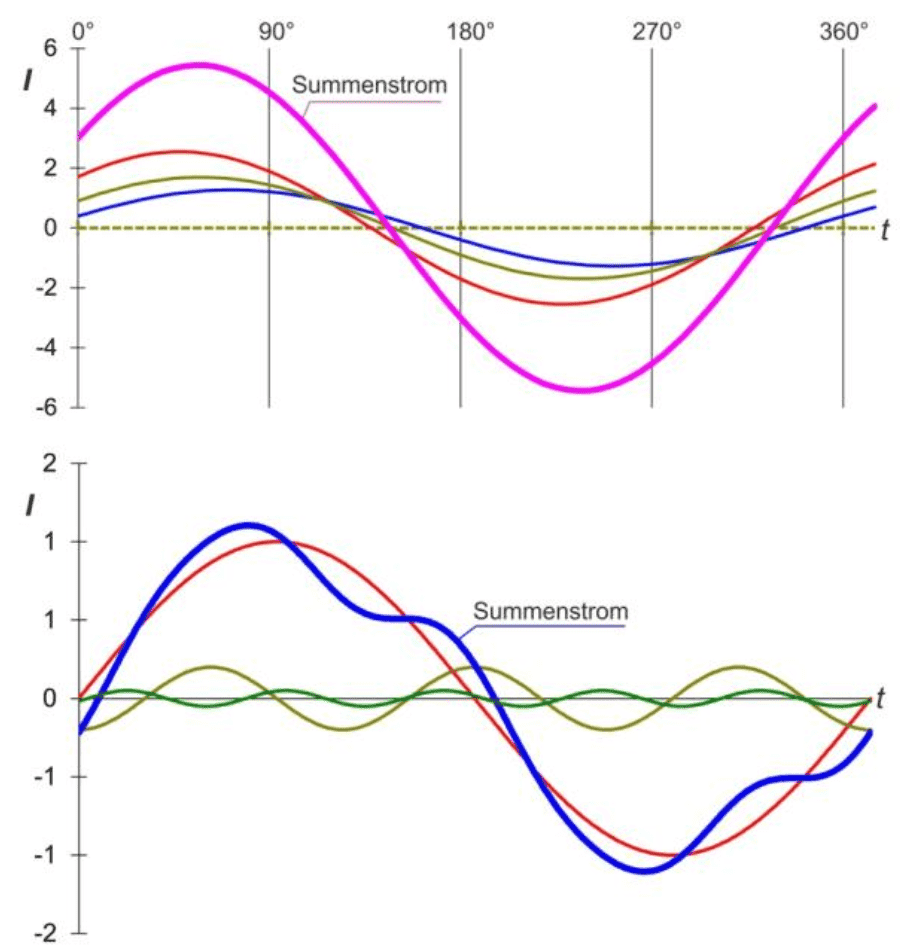
a) mit gleicher Frequenz
b) mit ungleicher Frequenz
Summe der Momentanwerte
Für das Drehstrom-Dreileiternetz mit gleichfrequenten sinusförmigen Strömen ist die Summe der zeitgleichen Momentanwerte idealerweise gleich null.
Effektivwert des Summenstromes
Für die Berechnung des Effektivwertes des Summen-stromes aus den Augenblickswerten von Strömen mit beliebiger Frequenz/Kurvenform gilt:
I_{\sum} = \sqrt{\frac{1}{T}\int_{T}^{0}(i_{0} +i_{1}+i_{2}+...+i_{n})^{2} dt }i_{0} +i_{1}+i_{2}+...+i_{n}Arithmetische Summe der zeitgleichen Stromanteile
Für die Berechnung ausschließlich aus den Effektivwerten von Strömen mit ungleicher Frequenz (z.B. Gleichanteil/ Grundschwingung mit Oberschwingungen) gilt auch:
I_{\sum} = \sqrt{I^{2}_{0} +I^{2}_{1}...+I^{2}_{n} }I0 = Effektivwert des Gleichstromes
I1 = Effektivwert der Grundschwingung
In = Effektivwert der höchsten Oberschwingung