Winkelbestimmung von Spannungs- und Stromharmonischen

Grundlagen Leistungsfluss von Oberschwingungen

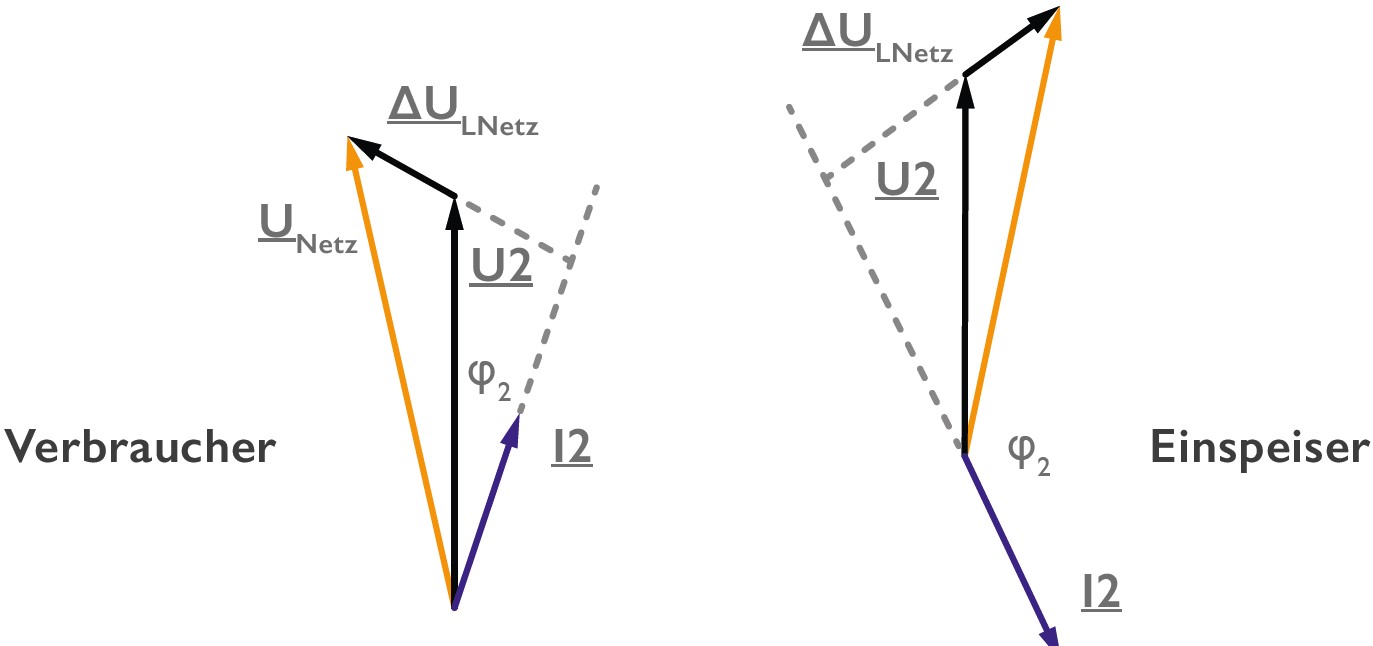
Die Leistungsflussrichtung von Oberschwingungen ist durch das Vorzeichen in der Wirkleistung bestimmt. Die Abbildung Nr. 1 zeigt das einphasige Ersatzschaltbild einer Netz- bzw. Verbraucheranordnung. Diese Abbildungen zeigen die dazugehörigen Zeigerdiagramme für zwei Energieflussrichtungen. Einmal Bezug und einmal Rückspeisung einer Leistung.

Die Wirkleistung berechnet sich bei reinen sinusförmigen Größen nach:

P_{2} = U_{2} * I_{2} * cosϕ_{2}

Die Formel für die Berechnung der Wirkleistung kann hierdurch für alle Frequenzen einfach berechnet werden. Das Vorzeichen der Wirkleistung wird alleine durch den Phasenwinkel ϕ bestimmt. In einem 50 Hz Wechselstromnetz ändert Strom und Spannung 100-mal pro Sekunde die Richtung und kann somit kein Vorzeichen haben.

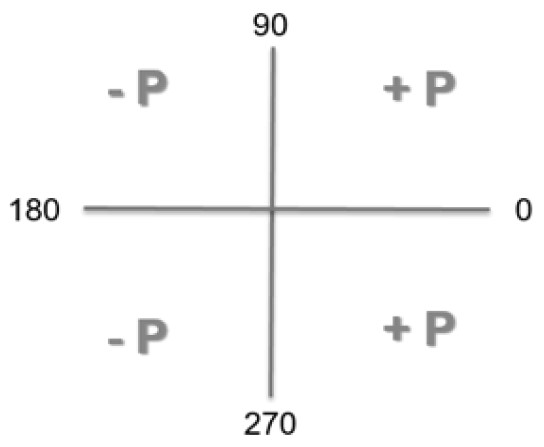
Im Winkelbereich 0 ≤ ϕ ≤ 90° sowie 270° ≤ ϕ ≤ 0° liegt eine Verbraucherstruktur vor und P erhält ein positives Vorzeichen.
Für 90° ≤ ϕ ≤ 270° errechnet sich P mit negativen Vorzeichen, es wird somit Leistung eingespeist per Definition.

Beispiel 1: Oberschwingungserzeuger in einem sauberen Netz

Der Verbraucher ist hier in einem reinen Sinusnetz ohne Oberschwingungen angeschlossen. Die Fouriertransformation in einem Power Quality Netzanalysator liefert an den Messpunkten sowohl die Amplitude als auch den Winkel der jeweiligen Harmonischen. Ist die Winkeldifferenz zwischen Strom und Spannung der gleichen Frequenz 90° ≤ ϕ ≤ 270° wirkt der Verbraucher bei dieser Harmonischen als Generator. Er speist per Definition diese Harmonische ins Netz ein. (verseucht somit das Netz)

Sinusförmige Netzspannung mit oberschwingungsbehafteten Strom
Aus der Definition der Wirkleistung ergibt sich mit einem oberschwigungsbehafteten Strom die Wirkleistung entsprechend:

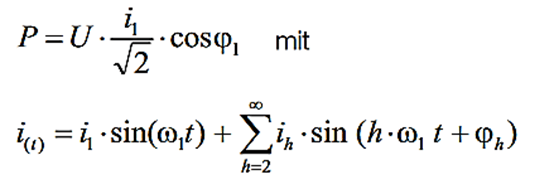
Daraus ist ersichtlich, dass nur die Stromgrundschwingung i1(t) die Wirkleistung bestimmt.

Beispiel 2: Strom und Spannung sind oberschwingungsbehaftet (reeles Beispiel wie in der Praxis üblich

Da jede Stromoberschwingung über die Impedanz aller Netzkomponenten wie Transformator und Leitungen eine entsprechende Spannungsharmonische hervorruft, ist dies der Standardfall in der Netzanalyse. Die Spannung besteht in diesem Fall analog dem Strom aus Grundschwingung und Oberschwingungen.

Mit dem Ansatz der nicht sinusförmigen Strombelastung und Spannung wird die Leistungsberechnung um einiges aufwendiger.

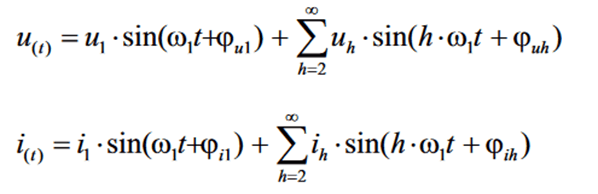
Achtung: Nur Spannungsharmonische und Stromharmonische gleicher Frequenz ergeben zusammen eine Wirkleistung!

Beispiel 3: Oberschwingungserzeuger in einem bereits mit Oberschwingungen verschmutzten Netz

Ist ein Verbraucher in einem Industrienetz angeschlossen, so erzeugen parallele Netze sowie benachbarte Verbraucher ebenso Oberschwingungen. Die Oberschwingungsspannung der einzelnen Harmonischen entsteht durch eine Überlagerung der einzelnen Komponenten. Dies beeinflusst sowohl die Amplitude als auch den Winkel des Vektors der Oberschwingungsspannung. Die nun gemessene Oberschwingungsleistung und damit die hieraus resultierende Richtung der Harmonischen wird stark von benachbarten Netzen und Verbrauchern beeinflusst. Häufig stärker als vom gemessenen Verbraucher selbst. Das Ergebnis dieser Messung ist in vielen Fällen sehr unzuverlässig.

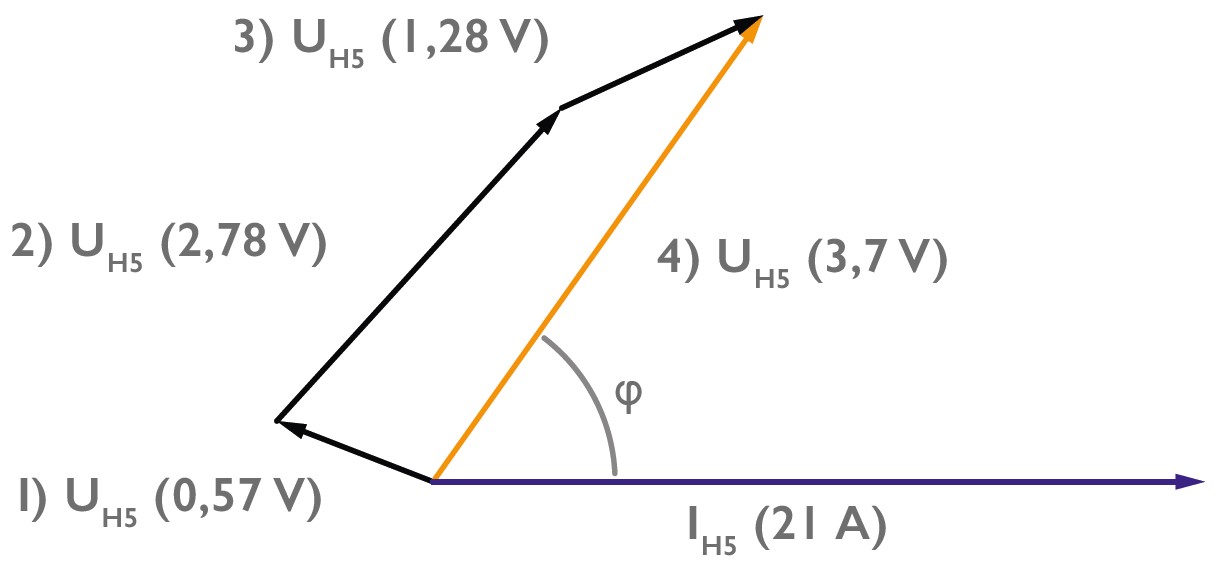
Abbildung 3 soll die vektorielle Addition der Netzrückwirkung verschiedener Störquellen aufzeigen.

Der Anlagenstrom einer Industrieanlage IH5 (rot) erzeugt mit seinen 21A an einer Netzimpedanz den Spannungsabfall „1) UH5“ mit 0,57V. Zu diesem Wert addieren sich vektoriell noch die 5. Spannungsharmonische, die im vorgelagerten Netz bereits anliegt „2) UH5“ mit 2,78V, sowie der Spannungsabfall der Verbraucherströme eines Bürogebäudes im gleichen Niederspannungsnetz „3) UH5“ mit 1,28V.

Der resultierende Spannungsabfall der vektoriellen Addition an der Messstelle ist im Beispiel grün gekennzeichnet „4) UH5“ mit 3,7V und ist in der Regel um einiges kleiner als die absolute Addition der Spannungsabfälle der unterschiedlichen Verbraucher.

Der Winkel ϕ der 5. Harmonischen wird in diesem Fall durch die anderen Verbraucher beziehungsweise der bereits bestehenden Vorbelastung im Netz sehr stark beeinflusst.

In diesem Beispiel befände sich der Winkel ϕ verursacht von Spannungsabfall des Anlagenstromes im 2. Quadranten und hätte somit eine negative Wirkleistung zur Folge. Da ein Netzanalysator aber nur die Summe aller Vektoren an der Messstelle „4) UH5“ messen kann, erhält man nun die Aussage einer positiven Wirkleistung da der Winkel ϕ durch andere Einflüsse in den 1. Quadranten verschoben wurde. Dies bedeutet in der Berechnung der Wirkleistung dieser 5. Harmonischen eine Umkehr des Leistungsflusses für diese Frequenz. Somit wurde aus einer Energieanlage, welche diese 5. Harmonische als Leistung ins Netz liefert (per Definition somit ein Erzeuger dieser Frequenz) nun eine Anlage geworden, welche diese Harmonische aus dem Netz geliefert bekommt.

Fazit

Man kann in den meisten Fällen nicht über die Leistungsflussrichtung einer Harmonischen auf den Verursacher dieser Frequenz schließen. Dies funktioniert nur in extremen Ausnahmefällen. Also nur, wenn das Energienetz nahezu keine Spannungsharmonischen aufweist und der Verbraucher, an dem der Netzanalysator angeschlossen ist und der die Stromoberschwingungen erzeugt, in diesem Netz die dominante Leistung besitzt. Alle anderen Verbraucher dürfen hier über ihre Oberschwingungsströme kaum Spannungsoberschwingungen erzeugen. Des Weiteren dürfen auch keine Spannungsharmonischen bereits aus dem vorgelagerten Mittelspannungsnetz importiert werden.

Winkelbestimmung von Harmonischen in Bezug zu einem Referenzphasor.

Es gibt in der Winkelbestimmung von Harmonischen eine alternative Bewertungsmethode.

Da die Wirkleistungsflussrichtung von Harmonischen in der Praxis häufig keine Aussage über den Verursacher dieser Frequenzen liefert und jeder Verbraucher, der heute keinen sinusförmigen Strom aus dem Netz bezieht, per se als Oberschwingungsquelle zu sehen ist, stellt sich vielmehr die Frage, wie sich diese vielen Quellen in Netz an ihrem Verknüpfungspunkt addieren. Werden sich diese für das Netz günstig (gegenseitig auslöschen) oder ungünstig vektoriell addieren?

Die Abbildung 4 zeigt als Beispiel, den Winkel der Stromharmonischen der 5. Ordnungszahl in Bezug auf die Grundschwingung der Spannung U1 (50Hz). Die meisten elektronischen Verbraucher verursachen Stromharmonische im Netz. Die Phasenlage der unterschiedlichen Geräte kann aber in verschiedenen Quadraten liegen, sodass sich diese Stromharmonischen in einem für das Energienetz günstigsten Fall auch gegenseitig kompensieren können.

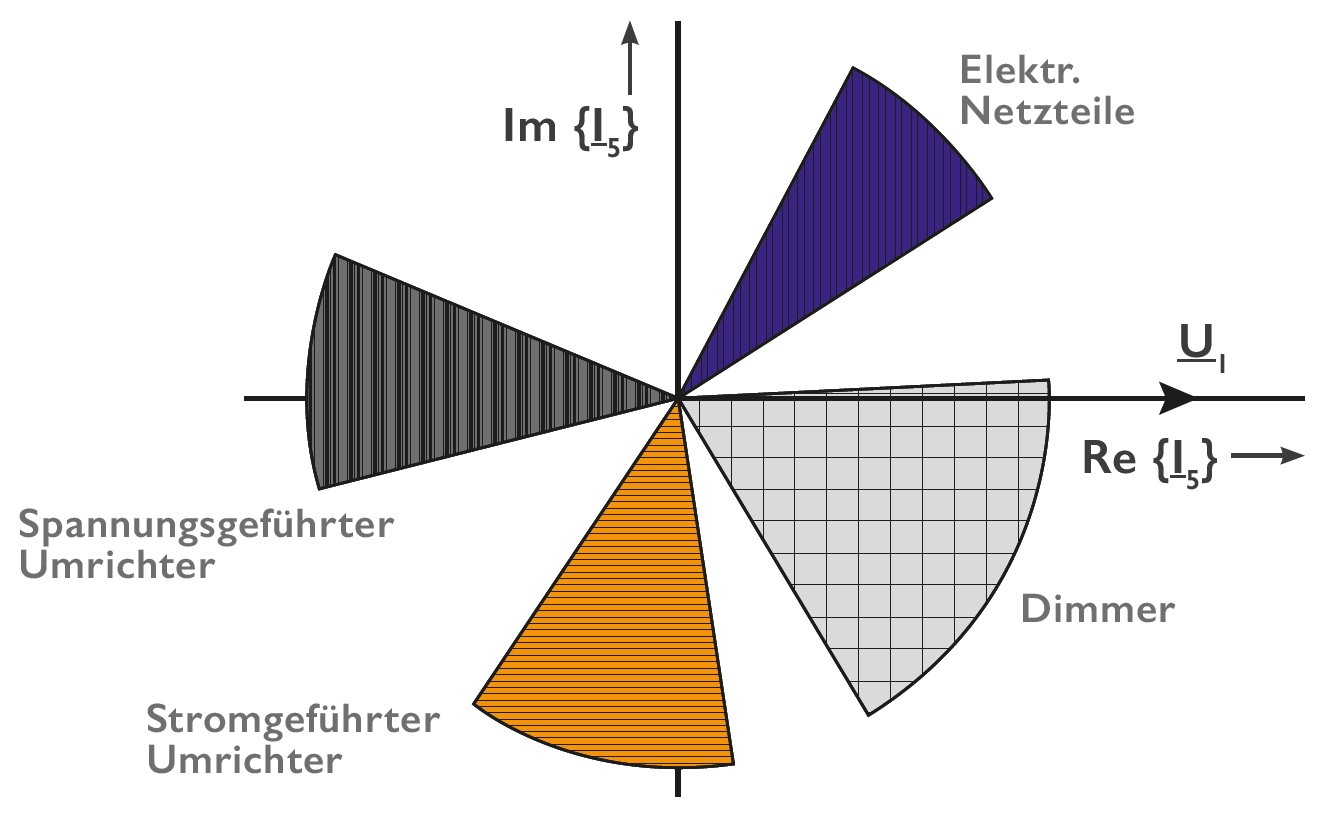
In der Abbildung 4 kann man erkennen, dass der Winkel der 5. Stromharmonischen von den meisten Schaltnetzteilen im 1. Quadranten in einem engen Winkelbereich liegen. Dies bedeutet zum Beispiel, dass sich alle in einem Bürogebäude betriebenen einphasigen Verbraucher fast linear aufaddieren. Sollte sich in diesem Gebäude aber auch eine 3-phasige Antrieb befinden, welcher über einen B6I Brückengleichrichter betrieben wird, so wird sich die 5. Stromharmonische am Verknüpfungspunkt beider Verbraucher gegenseitig kompensieren können. Somit werden in diesem Niederspannungsnetz zwar zwei eindeutige Oberschwingungsverursacher betrieben, beide gemeinsam erzeugen aber viel niedrigere Störpegel auf der Spannung als jeder einzelne für sich gesehen.

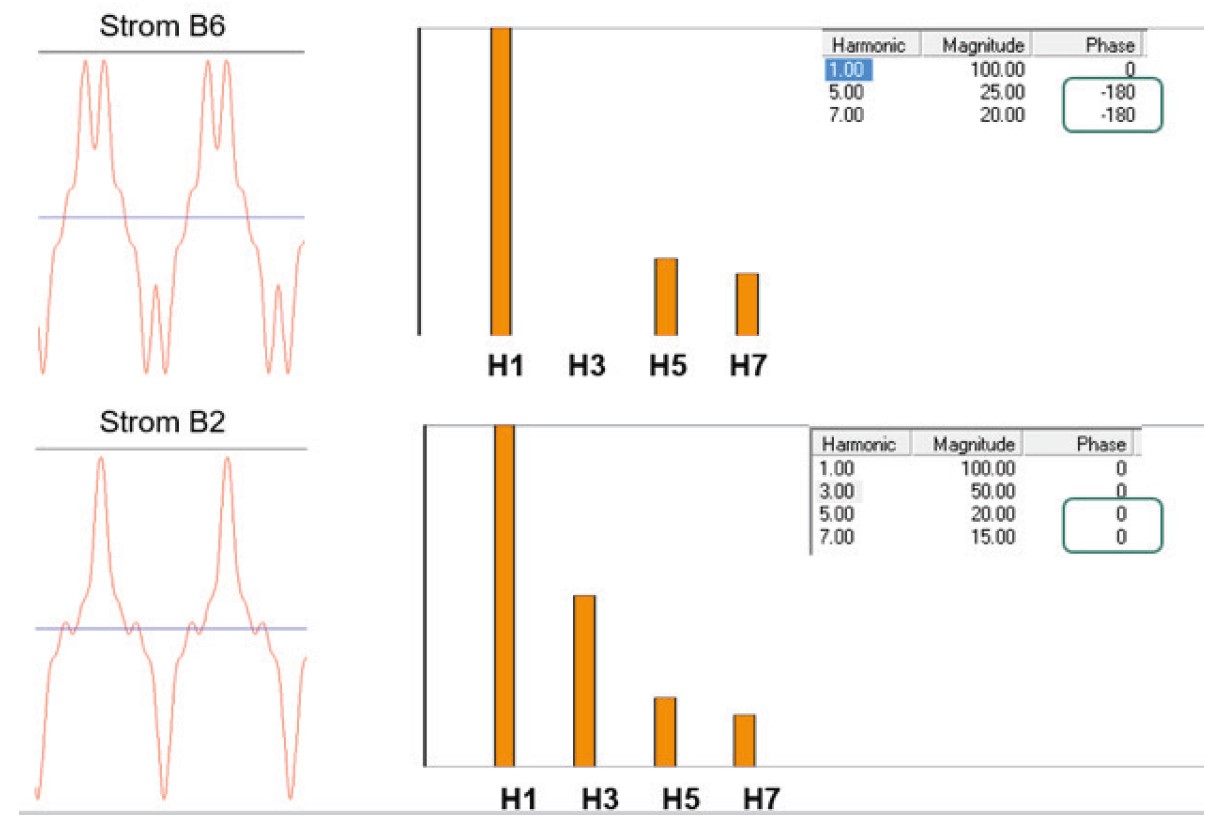
Die Winkellage der Harmonischen ist das Maß für die Lage dieser Frequenzen und hat Einfluss auf die Kurvenform. In dieser Simulation „Abbildung 5“ wurde die Stromkurve von einem B6-Brückengleichrichter sowie von einem typischen Schaltnetzteil nachgebildet. In beiden Fällen wurde auf die Stromgrundschwingung 50Hz eine 5. und eine 7. Stromharmonische eingeprägt. Auffällig ist die unterschiedliche Phasenlage der 5. und der 7. Harmonischen. Diese liegen um 180° auseinander. Dies bedeutet in der Praxis, dass beide Verbraucherströme gemeinsam näher an einem perfekten Sinus liegen, als jeder einzelne Strom für sich gesehen. In den Bürogebäuden von A. Eberle Nürnberg als Beispiel, steigt der Pegel der 250Hz Spannungsharmonische aufgrund der sehr vielen einphasigen Verbrauchern wie Monitore, Server, Beleuchtungen, Messgeräte uvm., auf Werte von 4,8% an. Schaltet sich in den Sommermonaten eine 3-phasige Klimaanlage zu, ausgeführt als B6- Brückengleichrichter ohne Zwischenkreisdrossel, so sinkt der Pegel der 5. Spannungsharmonischen auf Werte von 2% und dies, obwohl die Klimaanlage für sich gesehen ein starker Oberschwingungsverursacher ist. Dieser wirkt aber in diesem Fall wie ein aktives Oberschwingungsfilter und wirkt sich somit sehr positiv auf die Spannungsqualität aus.

Alle mobilen und festinstallierten Power Quality Geräte von A. Eberle berechnen die Winkel der Stromharmonischen und Spannungsharmonischen in beiden bisher vorgestellten Berechnungsvarianten.

a) Phasenwinkel Phi der jeweiligen Ordnungszahl für jede Harmonische. Hieraus wird jeweils die Wirkleistung und Blindleistung für jede Frequenz mit Vorzeichen ermittelt.

b) Phasenwinkel Phi aller Spannungs.- und Stromharmonischen in Bezug zum Referenzphasor der Grundschwingungsspannung. So ist es möglich, die Rückwirkungen von mehreren Verbrauchern auf den gemeinsamen Netzanschluss zu bewerten.

Wie kann nun eine Winkeldifferenz zwischen zwei unterschiedlichen Frequenzen ermittelt werden, wenn sich zum Beispiel die dritte Harmonische dreimal so schnell im Vektordiagramm dreht?

Die Bewertung des Phasenwinkels zum Beispiel der 5. Stromharmonischen zur Grundschwingung der Spannung wird im Nulldurchgang der Grundschwingungsspannung ermittelt. Diese Winkelbestimmung ist zum Beispiel in der Norm IEC61000-3-12 (Grenzwerte für Oberschwingungsströme, verursacht von Geräten und Einrichtungen mit einem Eingangsstrom > 16A
und ≤ 75A je Leiter, die zum Anschluss an öffentliche Niederspannungsnetze vorgesehen sind) festgelegt.

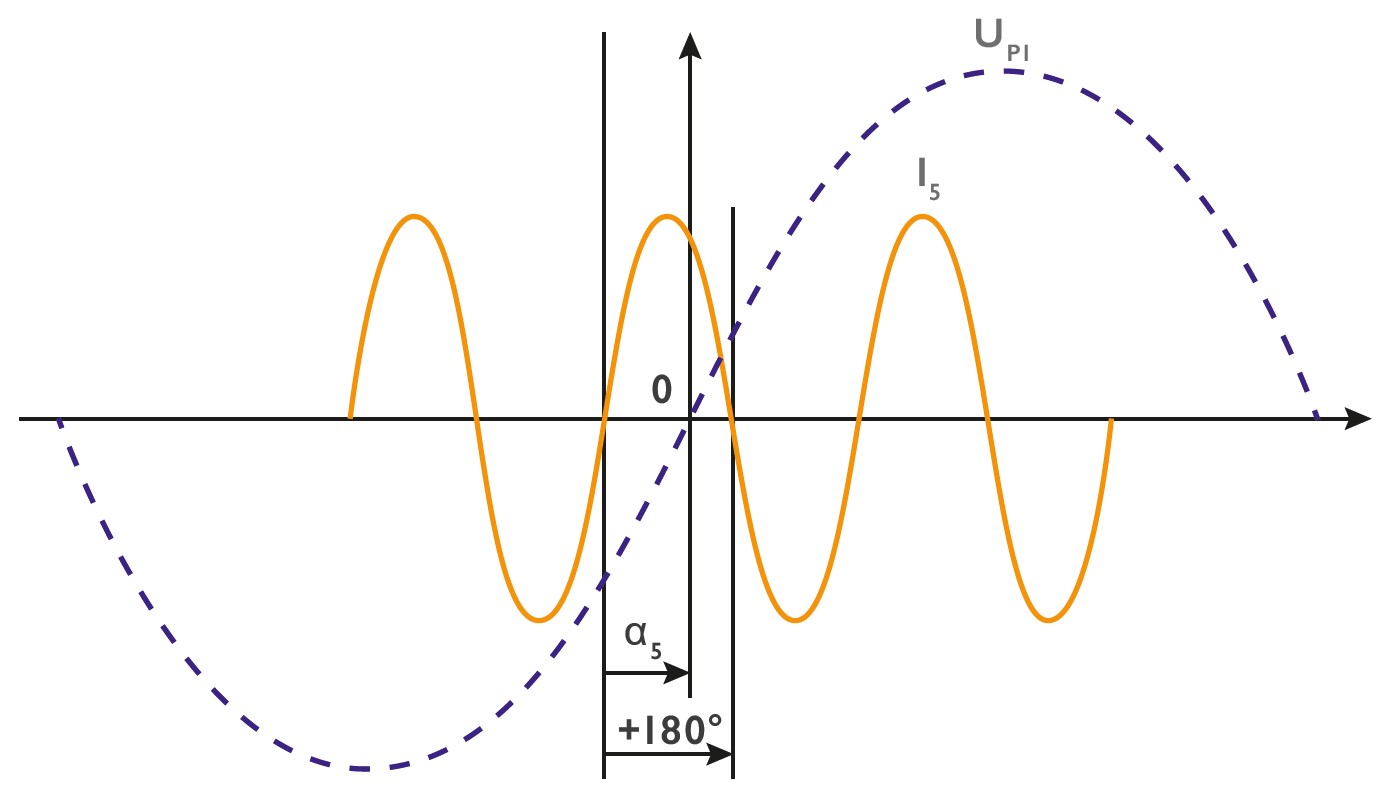
In diesem Bild eilt die 5. Stromharmonische der Spannungsgrundschwingung um den Phasenwinkel a voraus.

Berechnungsgrundlagen

Die Grundlage der Berechnung von Harmonischen ist in der Norm IEC61000-4-7 (Prüf- und Messverfahren zur Messung von Oberschwingungen und Zwischenharmonischen in Stromversorgungsnetzen und angeschlossenen Geräten) festgelegt. Hier wird aus einem Fenster über 10 Netzperioden (in 50Hz Netzen) bzw. 12 Netzperioden (in 60Hz Netzen) eine FFT Analyse berechnet. Diese ist zeitsynchron im Grundschwingungsnulldurchgang zu ermitteln. Ein Power Quality Netzanalysator nach IEC61000-4-30 Klasse A synchronisiert somit die Abtastrate stetig auf Netz Nulldurchgänge. Somit beträgt das Berechnungsfenster für die FFT Analyse nur ca. 200ms und ist von der Schwankung der Netzfrequenz abhängig. Aus der FFT Analyse erhält man ein Spektrum mit einer Auflösung von 5 Hz, mit Beträgen und Winkeln aller Harmonischen.

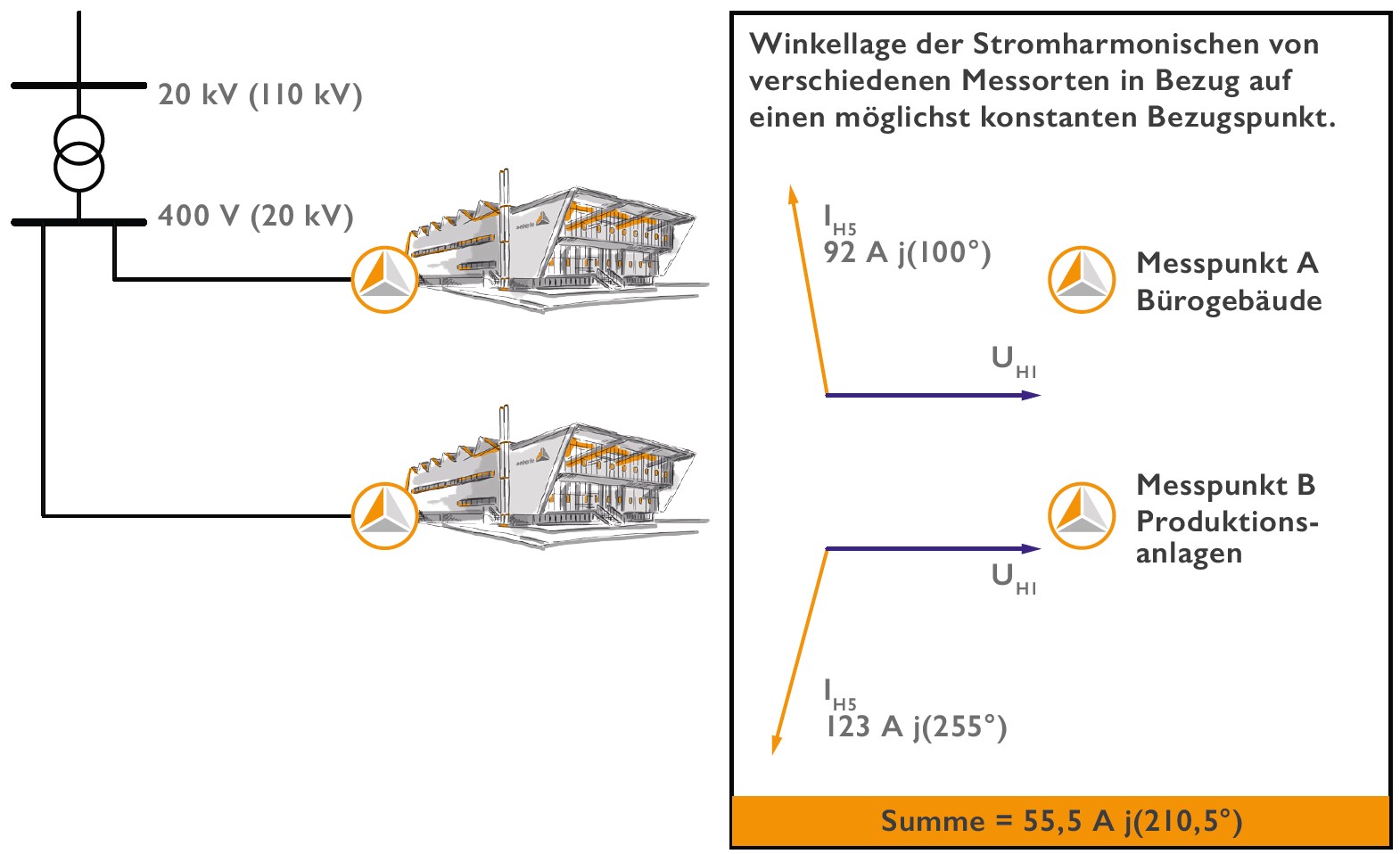
Ein Beispiel aus der Praxis wird in der Abbildung 7 dargestellt. In einem Industriepark mit mehreren Gebäuden, welche über einen Transformator versorgt werden, sollen die Auswirkungen der Stromharmonischen der einzelnen Kundenanlagen untersucht werden. Als Rechenbeispiel werden hier die Messwerte für die 5. Harmonische der Phase L1 verwendet.

Messpunkt Kundenanlage A war ein Bürogebäude mit vorwiegend einphasigen Verbrauchern wie PC´s, Monitore und Beleuchtungen. Hier wurde ein Strom der 5. Harmonischen von 92 A j(100°) gemessen. Der Messpunkt B lag am Übergabepunkt einer Produktionsanlage mit überwiegend frequenzumrichtergeregelten Antrieben. Hier wurde zu einem identischen Zeitpunkt parallel ein Stromwert der 5. Harmonischen von 123A j(255°) erfasst.

Laufen beide Verbraucheranlagen gemeinsam, so fließen am Transformator nicht die Summenströme beider Anlagen von 215A. Die am Transformator auftretenden Ströme lassen sich über eine komplexe Addition der Ströme mit Betrag und Winkel ermitteln und betragen in diesem Fall nur 55A j(210,5°).

Dies wäre ein günstiger Fall für das Netz, da sich die verschiedenen Verbrauchergruppen hier teilweise kompensieren. Jede Anlage, für sich alleine gesehen, würde den Transformator mit einem höheren Oberschwingungsstrom belasten.

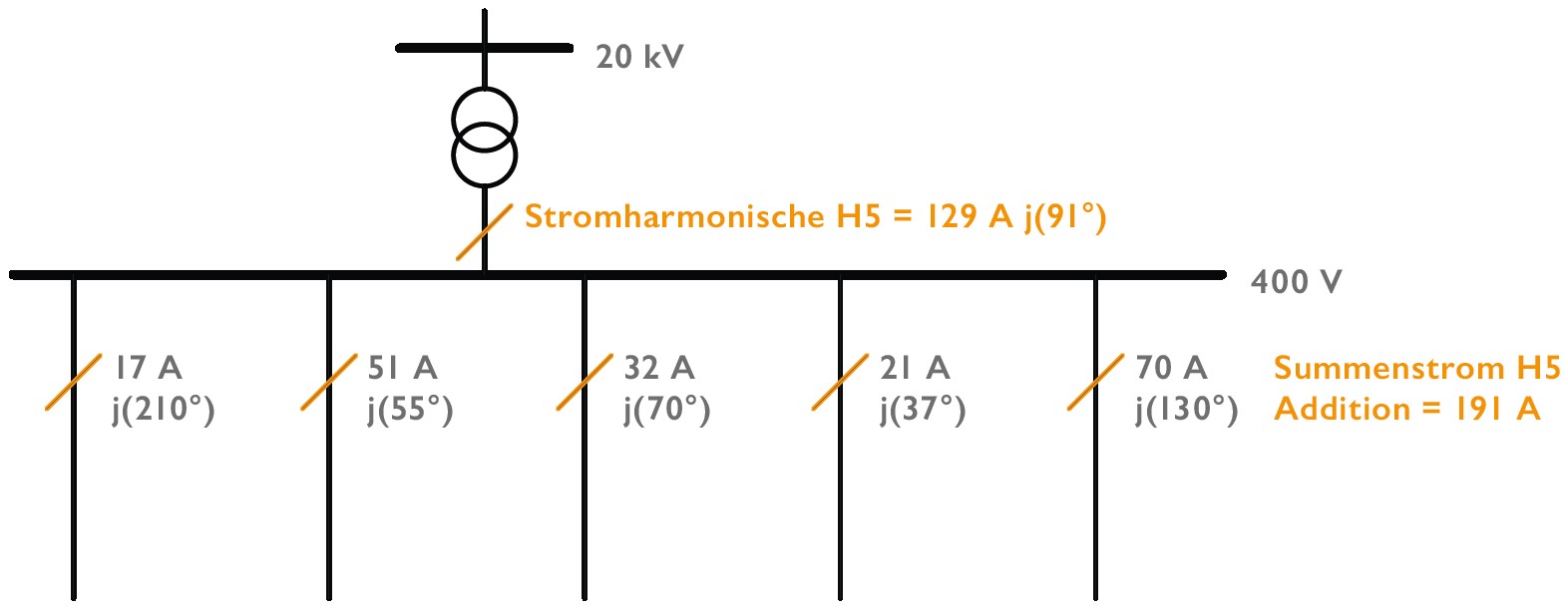
In einem weiteren Messbeispiel (Abbildung 8) sollten in einem Industrienetz mit sehr hohen Oberschwingungspegeln auf der Spannung, Maßnahmen ermittelt werden um diese Pegel sinnvoll zu reduzieren.

Die Spannungsgrenzwerte der 5. Harmonischen lagen in dieser Fertigungsanlage über dem Grenzwert von 6% und es traten erste Ausfälle in Produktionsanlagen auf. Mit einer PQ-Box 150 wurde jeder einzelne Kabelabgang, auf denen jeweils unterschiedliche Verbraucher angeschlossen waren, auf Stromoberschwingungen bewertet. Die PQ-Box gibt nun für jeden Abgang den Betrag sowie den Winkel in Bezug zur Grundschwingung der Spannung aus. Würde man in diesem Beispiel wieder alle Ströme der 5. Harmonischen linear aufaddieren, so ergäben sich Ströme von 191A an der Sammelschiene und am Transformator. Da auch an der Zuleitung zur Niederspannungssammelschiene eine PQ-Box installiert war, konnte hier ein Wert von nur 129A für die 5. Stromharmonische gemessen werden. Addiert man nun alle Werte der Kabelabgänge mit Betrag und Phase, so kommt man exakt auf den Wert, den man ebenso am Transformator misst. Durch die sehr unterschiedlichen Verbraucher auf den einzelnen Abgängen wie, Ladegeräte für Gabelstabler, Beleuchtungen und Antriebstechnik für die Produktion, liegen die Winkel in sehr unterschiedlichen Quadranten. Somit gibt es an dieser Niederspannungssammelschiene Verbraucher, welche für das Netz bereits als aktive Kompensation von Oberschwingungspegel fungieren und andere Verbraucher, welche die bereits hohen Pegel auf der Spannung noch verstärken.

Darstellungsarten in Auswertesoftware WinPQ mobil

Die Auswertesoftware WinPQ mobil bietet eine Vielzahl von Darstellungsmöglichkeiten für die Analyse von Spannungs- und Stromharmonischen. Dies jeweils für Langzeitaufzeichnungen über Tage oder Wochen oder für eine direkte Onlineanalyse.

Die Abbildung 9 zeigt ein Beispiel einer Onlineanalyse der Winkel der Spannungs- und Stromharmonischen in Bezug zum Referenzphasor Grundschwingung Phase L1 (Vektor bei 0° Phasenlage)

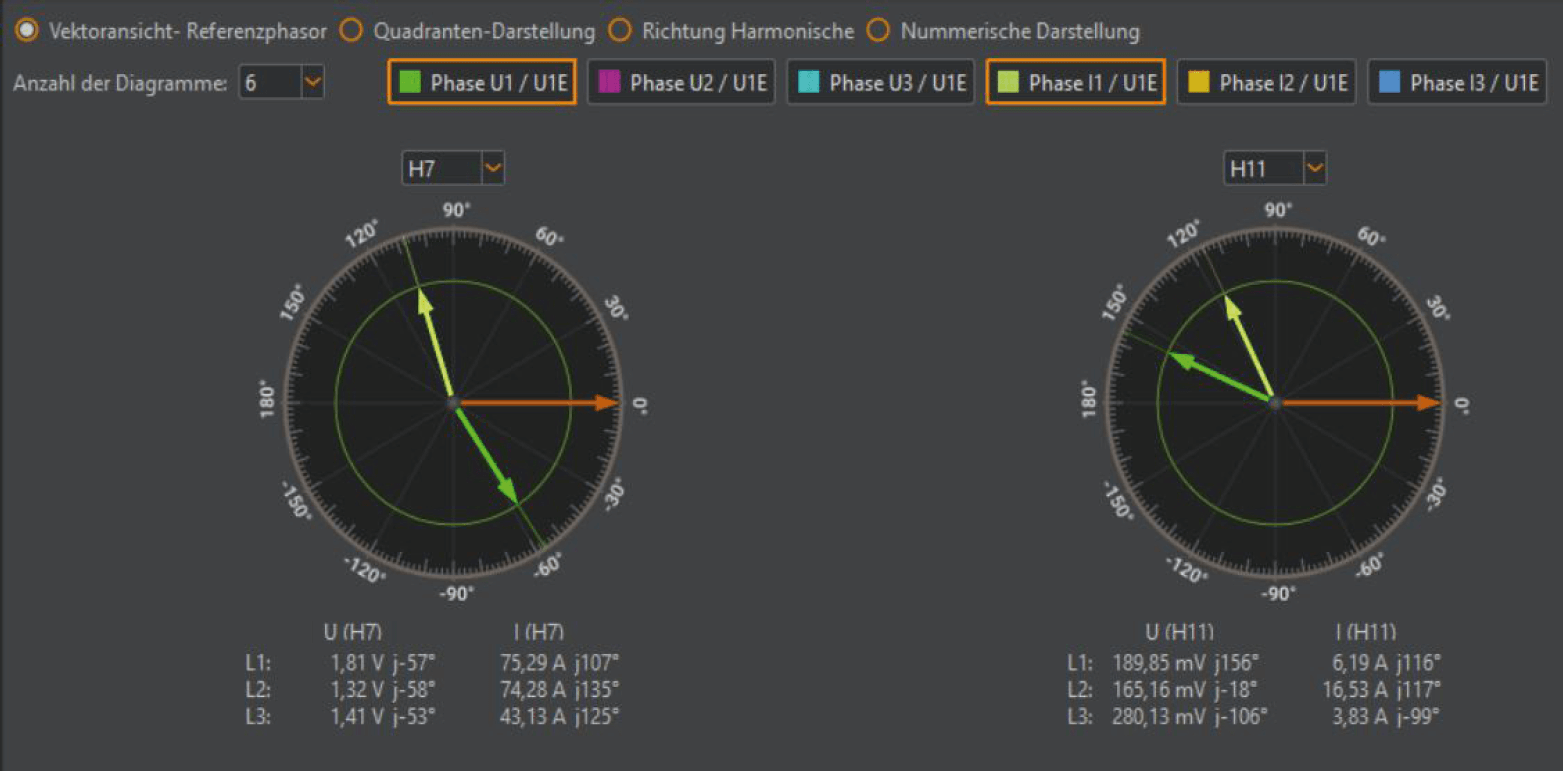
Aussage dieser Anzeige in WinPQ mobil:

Die Stromharmonische H7 von diesem angeschlossenen Verbraucher wirkt sich günstig auf das vorbelastete Netz aus. Man erkennt dies an der Differenz des Phasenwinkels der Vorbelastung im Netz (hier grüner Vektor mit 1,22V) und nahezu 180° Phasendifferenz zum Oberschwingungsstrom (gelber Vektor mit 15,6A).

Eine gegenteilige Aussage erhält man bei diesem gemessenen Verbraucher für die 11. Stromoberschwingung. Hier wird der bereits bestehende Pegel auf der Spannung durch diese Anlage verschlechtert.

Der Winkelbezug aller Harmonischen ist auf die Grundschwingung des entsprechenden Leiters bezogen. Das bedeutet das zum Beispiel der Winkel 7. Stromharmonischen von L2 auch auf die Grundschwingung der Phase L2 bezogen ist. Dies hat den Vorteil das man für alle drei Phasen einer Strom- oder Spannungsharmonischen identische Winkel erhält. Würden alle Harmonischen immer auf die Grundschwingung der Phase L1 bezogen werden, so müsste man die Phasenverschiebung der einzelnen Leitern mit 120° zusätzlich beachten. Eine Aussage, ob sich ein Verbraucher an seinem Anschluss günstig oder ungünstig auswirkt, geht aber über beide Wege unabhängig.

Anzeige der Leistungen und Quadranten in Bezug auf den Winkel phi der Harmonischen

Abbildung 10 zeigt eine weitere Darstellungsart in WinPQ mobil und stellt die Wirkleistung jeder Harmonischen mit Vorzeichen und Phasenlage im Quadranten dar. Ein negatives Vorzeichen der Wirkleistung bedeutet mathematisch ein Energiefluss vom Verbraucher in das vorgelagerte Netz. An dieser Stelle erscheinen auch noch die Scheinleistungen und Blindleistungen aller Harmonischen.

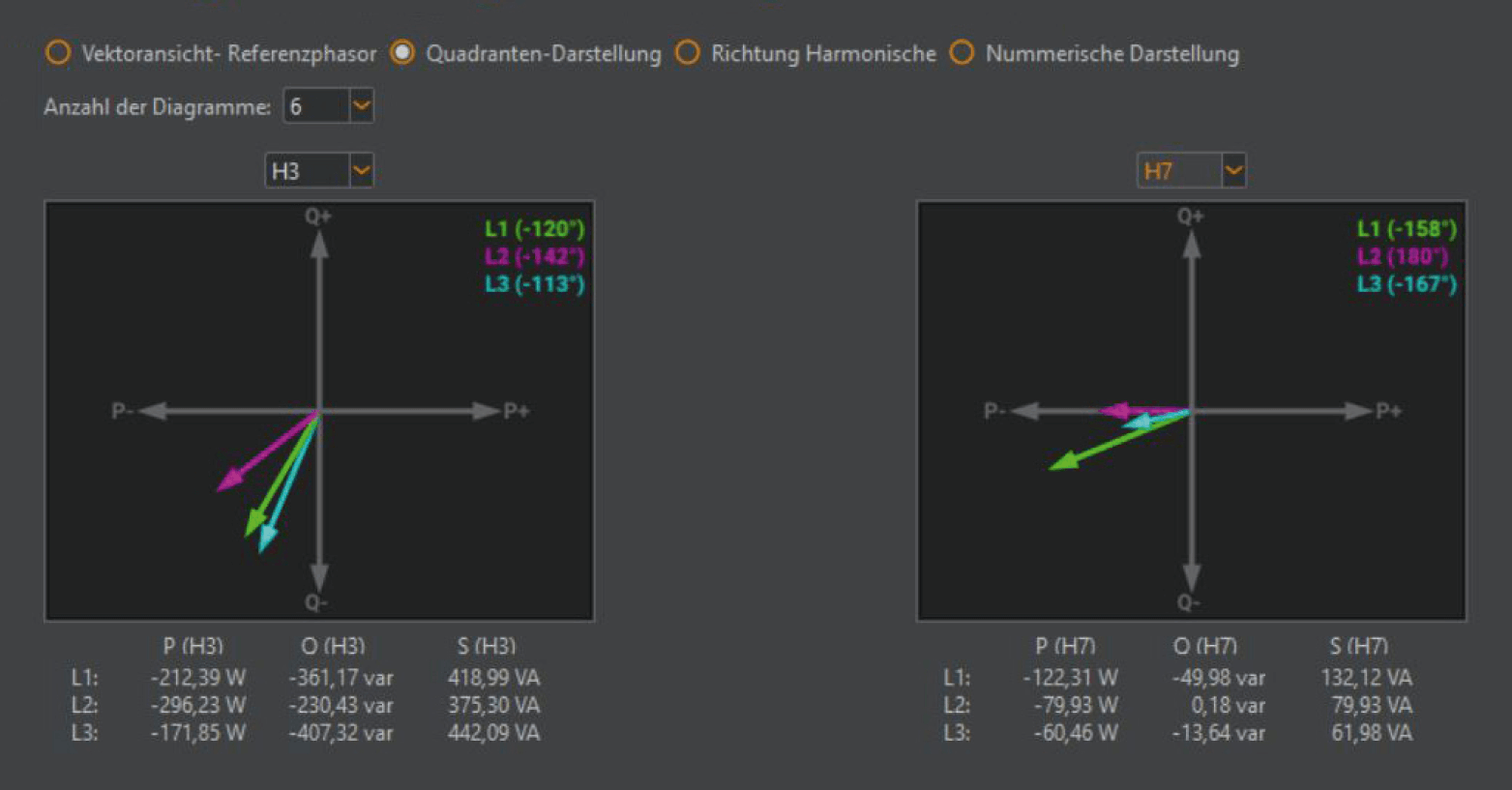
Spannungsharmonische und Stromharmonische gleicher Frequenz ergeben eine Wirkleistung:

So wie für die Grundschwingungsleistung kann für jede Harmonische auch eine Wirkleistung berechnet werden. Bedingung ist, wie bereits anfangs erklärt, eine Wirkleistungsberechnung immer nur für gleiche Frequenzen. Da der Phasenwinkel ϕ das Vorzeichen der Wirkleistung umdrehen kann, wäre es mathematisch möglich, dass eine Anlage eine höhere Grundschwingungswirkleistung aus dem Netz bezieht, als man dann im Messgerät oder auch Energiezähler angezeigt bekommt.

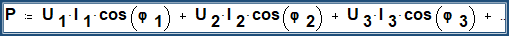
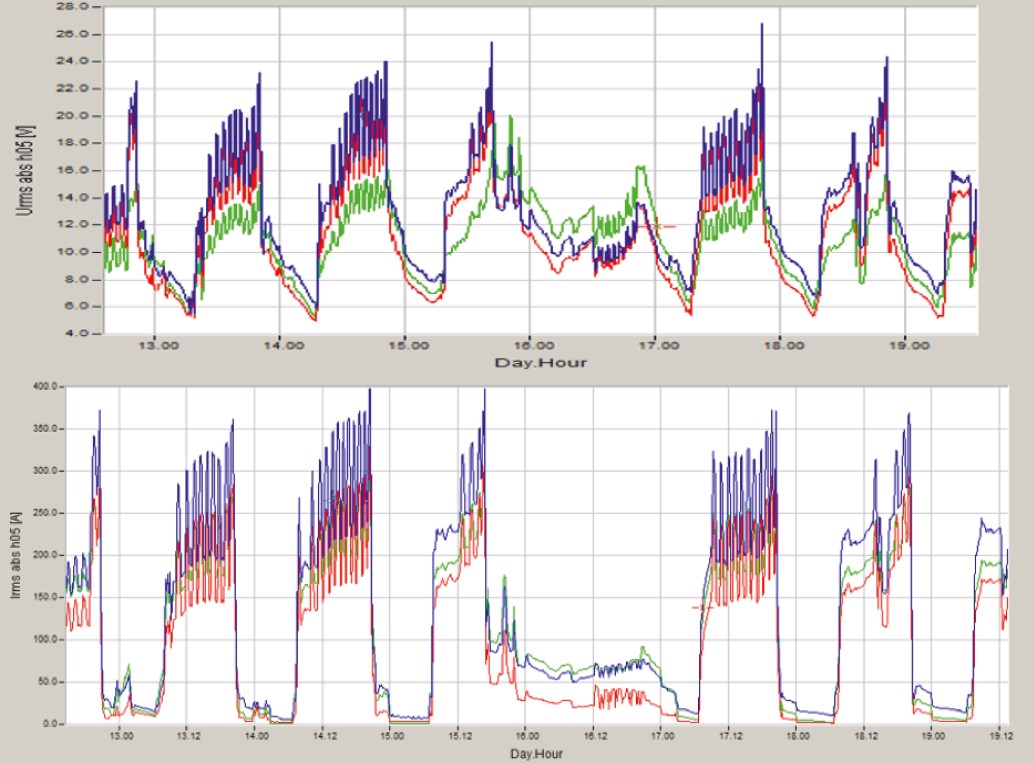
Hier ein reelles Beispiel aus der Praxis, in der eine Bewertung der Leistungsflussrichtung eine Rolle spielen könnte. Grund für diese Messung waren Unterschiede in der Energiemessung zwischen verschiedenen geeichten Energiezählern.

In dieser Anlage wurden sehr große B6-Brückengleichrichter installiert, welche sehr hohe Werte der 5. Stromharmonischen von bis zu 400A in Summe erzeugt haben.  Diese großen Oberschwingungsströme erzeugten im Netz eine 5. Spannungsharmonische von bis zu 26V.

Aus diesen hohen Spannungswerten und Stromwerten der 5. Harmonischen ergibt sich über die Formel der Leistungsberechnung eine Wirkleistung von max. 23kW.

P_{2} = U_{2} * I_{2} * cosϕ_{2}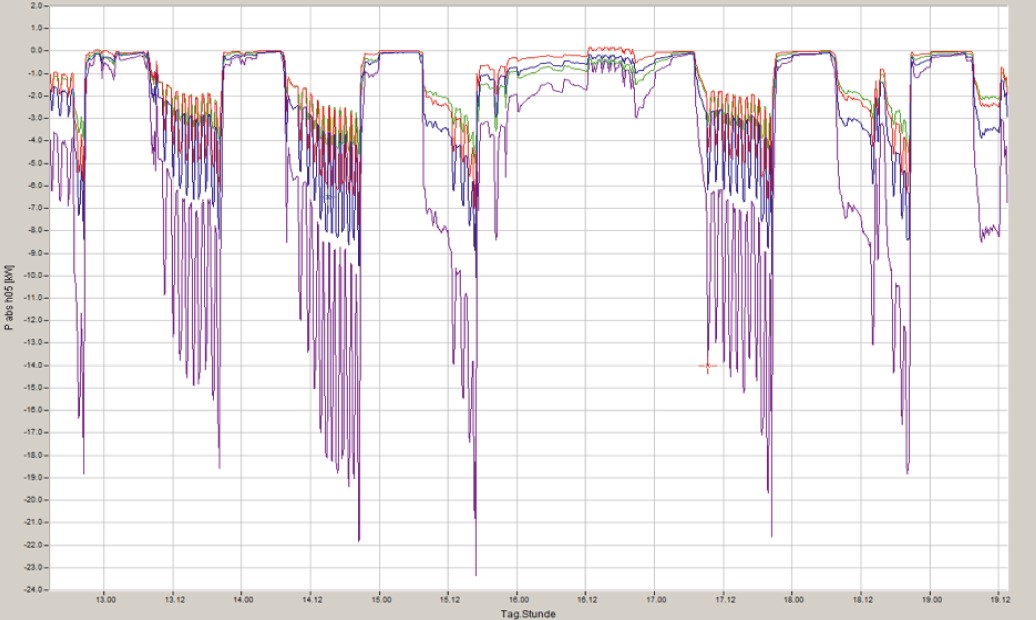

In der gemeinsamen Darstellung mit der Grundschwingungswirkleistung erkennt man das entgegengesetzte Vorzeichen der Wirkleistung der 5. Harmonischen Wirkleistung im Gegensatz zur Grundschwingungswirkleistung mit positiven Vorzeichen.

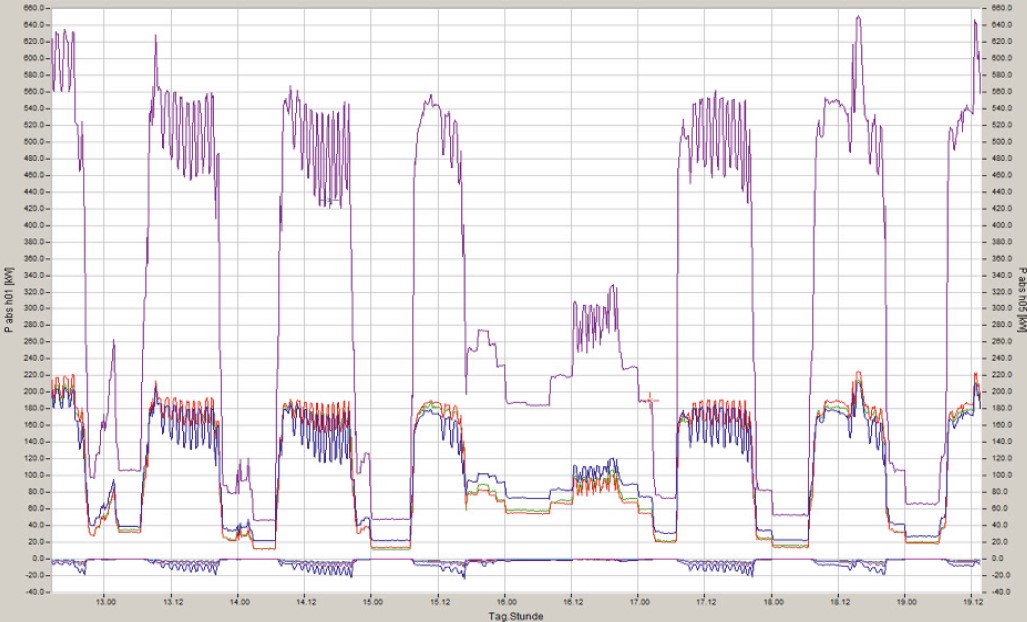
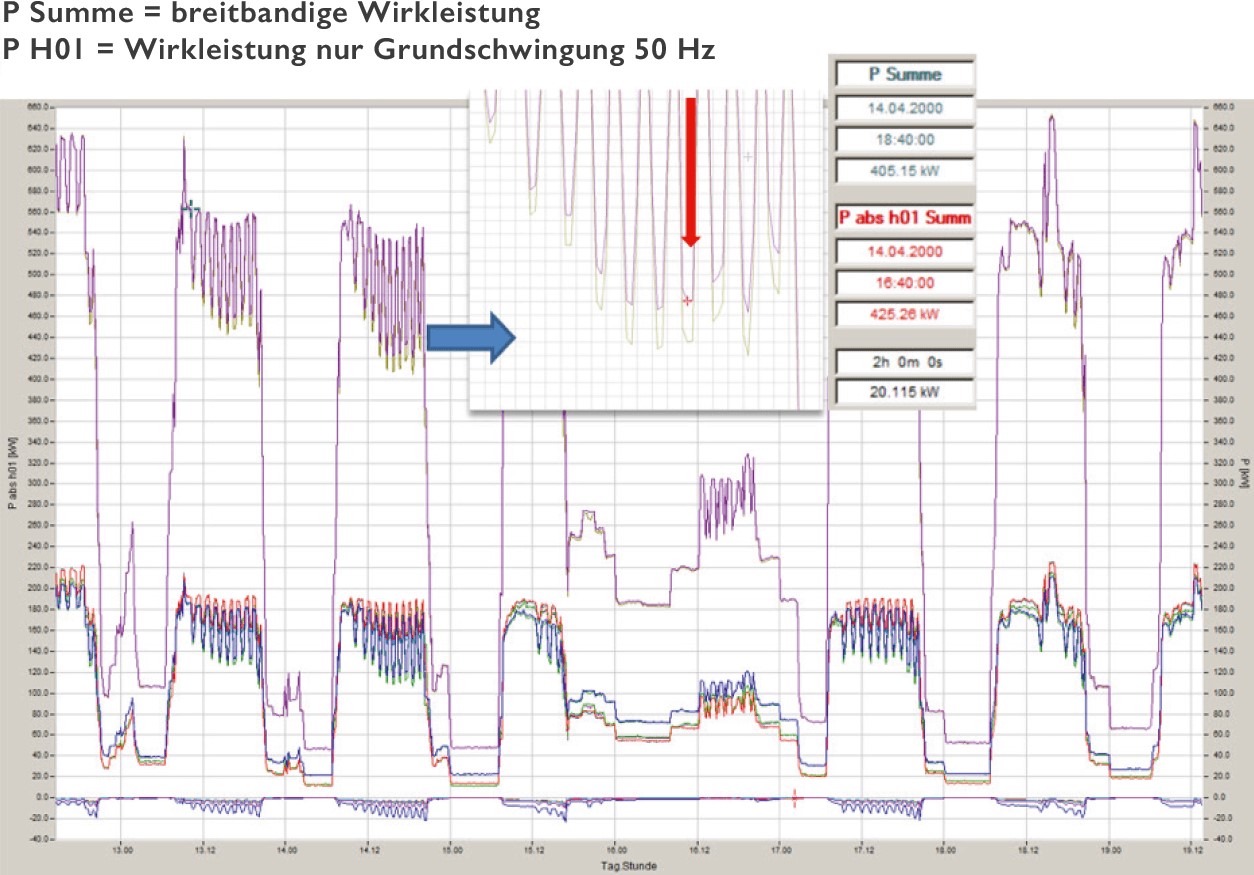
In dieser Darstellung in Abbildung 14 ist zu erkennen das diese Anlage eine 50Hz Wirkleistung aus dem Netz bezieht. Aufgrund der hohen Rückwirkungen der 5. Harmonischen auf Strom und Spannung ergibt sich eine negative Wirkleistung der 5. Harmonischen. Diese bewirkt eine Reduktion der breitbandig berechneten Wirkleistung dieser Anlage. Also den Leistungswert den auch ein elektronischer Zähler ermittelt. Ein Ferrariszähler der ebenfalls in dieser Verteilung angeschlossen war, hatte hier eine um einige Prozent höhere Wirkleistung erfasst.

Messfehler

Zu beachten ist das in den Messfehlern für die Winkelbestimmung von Harmonischen stark die Winkelfehler von Stromwandlern und Stromzangen eingehen. In Mittelspannungsmessungen kommen zusätzlich noch die Fehler von Spannungswandlern hinzu.

So verursacht zum Beispiel ein Winkelfehler eines Stromwandlers von 1°, einen Fehler von 15° Bezogen auf die 15. Harmonische. (15 x 50Hz)

Auch ist es nicht unerheblich welche Auflösung die A/D-Eingangswandler von einem Power Quality Netzanalysator besitzen. Auf der einen Seite müssen sehr hohe Ströme auf der Grundschwingung erfasst werden können vom Messgerät und Stromzangenset, auf der anderen Seite müssen sehr kleine Stromharmonische präzise aufgelöst werden. Hier zeigt sich ein großer Vorteil im Einsatz von 24bit Wandlern im Gegensatz zu 16bit-Eingangswandlern.