Información general
Para la conexión en paralelo de fuentes de alimentación, se aplica el principio de superposición, cuando todos los recursos tienen un comportamiento lineal. Este comportamiento es el caso de los transformadores de corriente dentro del rango de carga admisible y por debajo de unos pocos miles de hercios. Debe tenerse en cuenta que, en principio y técnicamente, sólo se suman los valores instantáneos simultáneos, ¡no los valores efectivos!
A través de la resistencia de carga común RL de los transformadores de corriente en paralelo fluye una corriente que corresponde a la suma aritmética de los valores instantáneos de todas las corrientes. Se supone que los transformadores de corriente proporcionan corrientes superpuestas y que no se superan los límites de frecuencia (orden superior de los armónicos).
La suma aritmética de los valores instantáneos no sólo depende de la cantidad, sino también del signo de las corrientes individuales, por lo que para la suma debe tenerse en cuenta la polaridad de las fuentes de corriente. Con corrientes alternas del mismo sentido de flujo de energía, la polaridad está relacionada con los terminales secundarios S1 (k) y S2 (l) del transformador de corriente.
Forma de onda de la corriente total
Cuando se suman corrientes sinusoidales de igual frecuencia, la curva de iS tiene la forma de una curva sinusoidal, con corrientes de frecuencia desigual la forma de onda de la corriente total i ya no es sinusoidal.
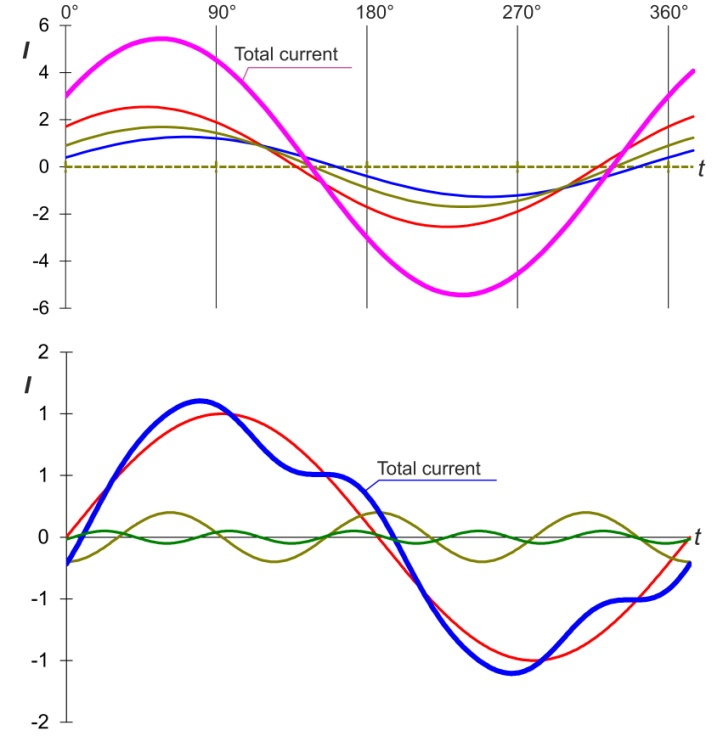
a) with the same frequency
b) with different frequencies
Suma de los valores instantáneos
Para la red trifásica de tres hilos con corrientes sinusoidales de la misma frecuencia, los valores instantáneos simultáneos son idealmente cero.
Valor efectivo de la corriente total
Para el cálculo del valor efectivo de la corriente total a partir de los valores momentáneos de corriente con una frecuencia/forma de onda arbitraria se aplica lo siguiente:
I_{\sum} = \sqrt{\frac{1}{T}\int_{T}^{0}(i_{0} +i_{1}+i_{2}+...+i_{n})^{2} dt }i_{0} +i_{1}+i_{2}+...+i_{n}Suma aritmética de los componentes simultáneos de corriente
Para el cálculo sólo de los valores efectivos de corrientes con frecuencias diferentes (por ejemplo, igual valor/ fundamental con armónicos) también se aplica lo siguiente:
I_{\sum} = \sqrt{I^{2}_{0} +I^{2}_{1}...+I^{2}_{n} }I0 = Valor efectivo de la corriente continua
I1 = Valor efectivo de la fundamental
In = Valor efectivo del armónico más alto